In meccanica quantistica il momento angolare magnetico nella direzione z è dato da $L_z=m_I\hbar$. Il kernel con $m_I=1/2$ ha $L_z=1/2\hbar$, mentre il kernel con $m_I=-1/2$ ha $L_z=-1/2\hbar$. Il momento magnetico in questa direzione è $\mu_z=\gamma L_z$.

Queste equazioni ci permettono di determinare l'energia di entrambi i livelli. \begin{equation}\label{ec4} E=-\mu_zB_0=-\gamma m_I\hbar B_0 \end{equation} Ora possiamo calcolare la differenza di energia tra i due livelli \begin{equation}\label{ec6} \ Delta E=-\gamma (-1/2)\hbar B_0 + \gamma 1/2\hbar B_0=\gamma\hbar B_0 \end{equazione}

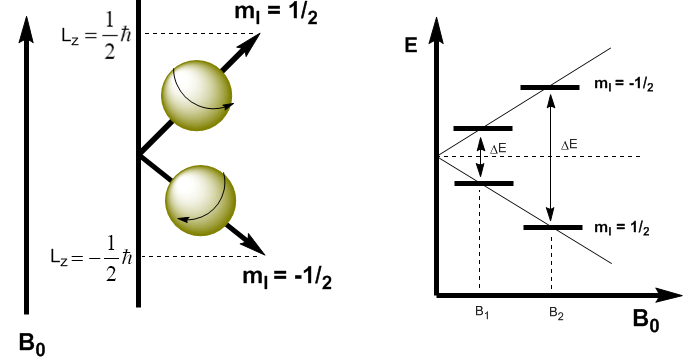
Come si può vedere nell'equazione (\ref{ec6}) la differenza di energia dipende dal campo magnetico applicato. Se il campo magnetico è basso, $\Delta E$ è piccolo e anche la differenza di popolazione tra i due livelli è piccola, il che causa un problema di sensibilità. A campi magnetici elevati abbiamo una separazione significativa tra i livelli, che dà origine a un'elevata differenza di popolazione, ottenendo una maggiore sensibilità.