Dettagli

Germán Fernández

Risonanza Magnetica Nucleare (NMR)

Visite: 13336

I nuclei atomici ruotano su se stessi (spin) e presentano un momento angolare che è dato dall'espressione \begin{equation}\label{ec1} L=\sqrt{I(I+1)}\hbar \end{equation} Momento angolare dipende dal numero quantico I (numero quantico momento angolare o spin nucleare), che può assumere valori diversi a seconda del tipo di nucleo, I=0, 1/2, 1, 3/2, 2, 5/2, 3,.....

Il calcolo del numero quantico di spin per un nucleo viene effettuato sommando gli spin di protoni e neutroni spaiati. Ad esempio, l'idrogeno ha I=1/2, poiché è composto da un solo protone.

Gli stati di spin quantistici consentiti sono dati da $m_I$, che assume i seguenti valori \begin{equation}\label{ec2} m_I=-I, -I+1, ...., I-1, I \end{equation} Il numero di valori che $m_I$ assume per un dato valore di I è $2I+1$. Quindi, per un nucleo con I=1/2 ci sono due possibili stati quantistici di spin dati da $m_I=-1/2, 1/2$. Un nucleo con I=1 ha tre stati spin quat consentiti $m_I=-1, 0, +1$. In assenza di un campo magnetico, gli stati quantici di spin sono degeneri.

Dettagli

Germán Fernández

Risonanza Magnetica Nucleare (NMR)

Visite: 13797

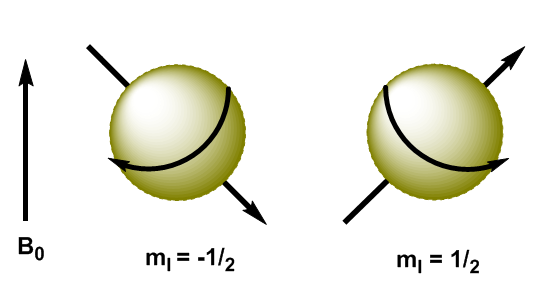
I nuclei atomici sono particelle cariche e il loro momento angolare produce momento magnetico, rappresentato da $\mu$ \begin{equation}\label{ec3} \mu=\gamma L = \gamma \sqrt{I(I+1)} \hbar \end{equation} dove $\gamma$ è la costante giromanetica, caratteristica di ogni nucleo. Quando applichiamo un campo magnetico, $B_0$, a nuclei con I=1/2, i momenti magnetici sono orientati in modo tale che i nuclei con $m_I=1/2$ abbiano il loro momento magnetico allineato con il campo e il i nuclei con $ m_I=-1/2$ hanno il loro momento magnetico opposto al campo applicato.

Dettagli

Germán Fernández

Risonanza Magnetica Nucleare (NMR)

Visite: 11225

In meccanica quantistica il momento angolare magnetico nella direzione z è dato da $L_z=m_I\hbar$. Il kernel con $m_I=1/2$ ha $L_z=1/2\hbar$, mentre il kernel con $m_I=-1/2$ ha $L_z=-1/2\hbar$. Il momento magnetico in questa direzione è $\mu_z=\gamma L_z$.

Queste equazioni ci permettono di determinare l'energia di entrambi i livelli. \begin{equation}\label{ec4} E=-\mu_zB_0=-\gamma m_I\hbar B_0 \end{equation} Ora possiamo calcolare la differenza di energia tra i due livelli \begin{equation}\label{ec6} \ Delta E=-\gamma (-1/2)\hbar B_0 + \gamma 1/2\hbar B_0=\gamma\hbar B_0 \end{equazione}

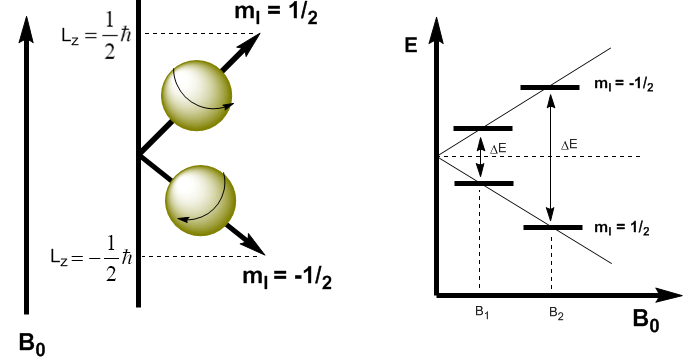
Come si può vedere nell'equazione (\ref{ec6}) la differenza di energia dipende dal campo magnetico applicato. Se il campo magnetico è basso, $\Delta E$ è piccolo e anche la differenza di popolazione tra i due livelli è piccola, il che causa un problema di sensibilità. A campi magnetici elevati abbiamo una separazione significativa tra i livelli, che dà origine a un'elevata differenza di popolazione, ottenendo una maggiore sensibilità.

Dettagli

Germán Fernández

Risonanza Magnetica Nucleare (NMR)

Visite: 13388

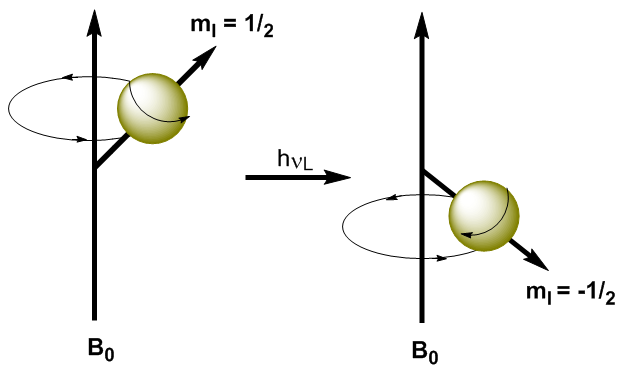
Applicando radiazioni elettromagnetiche di opportuna frequenza (onde radio) è possibile promuovere i nuclei dal livello energetico inferiore ($m_I=1/2$) al livello energetico superiore ($m_I=-1/2$). Quando la radiazione elettromagnetica e la precessione del nucleo entrano in risonanza, avviene l'assorbimento. Possiamo calcolare la frequenza di risonanza (frequenza di Larmor) usando l'equazione di Planck. \begin{equation}\label{ec7} \Delta E = h\nu_L \end{equation} Sostituendo la differenza di energia per l'equazione (\ref{ec7}) \begin{equation}\label{ec8} \gamma\ hbar B_0=h\nu_L \end{equation} Risoluzione per la frequenza di Larmor \begin{equation}\label{ec10} \nu_L=\frac{\gamma}{2\pi}B_0 \end{equation} Come si può vedere nell'equazione (\ref{ec10}) la frequenza alla quale avviene la transizione dipende dal campo magnetico applicato. L'aumento del campo magnetico produce un aumento della differenza di energia tra i livelli di spin, quindi è necessaria una radiazione di frequenza più elevata per produrre la transizione.

Dettagli

Germán Fernández

Risonanza Magnetica Nucleare (NMR)

Visite: 16541

Nella risonanza magnetica vengono utilizzati nuclei con momento angolare di spin diverso da zero, come $^1H$ e $^{13}C$. Tuttavia, le frequenze di risonanza non sono le stesse per tutti i nuclei di idrogeno o carbonio, dipendono dall'ambiente chimico che circonda ciascun nucleo. Ciò è dovuto al fatto che gli elettroni che circondano ogni nucleo generano un campo magnetico opposto a quello applicato, si dice che i nuclei sono schermati, dove $\sigma$ è la costante di schermatura. \begin{equation}\label{ec11} B_{eff}=B_0-\sigma B_0=(1-\sigma)B_0 \end{equation} $B_{ef}$ è il campo magnetico netto che agisce sul protone; $B_0$ è il campo magnetico applicato; $\sigma$ è la costante di schermatura, indipendente dal campo applicato. In questa nuova situazione, con i nuclei schermati dalla densità elettronica circostante, la frequenza di risonanza diventa \begin{equation}\label{ec12} \nu=\frac{\gamma}{2\pi}(1 -\sigma)B_0 \end{equation} Nuclei con ambienti chimici diversi hanno una costante di schermatura diversa, generando segnali diversi nello spettro NMR.

Dettagli

Germán Fernández

Risonanza Magnetica Nucleare (NMR)

Visite: 21886

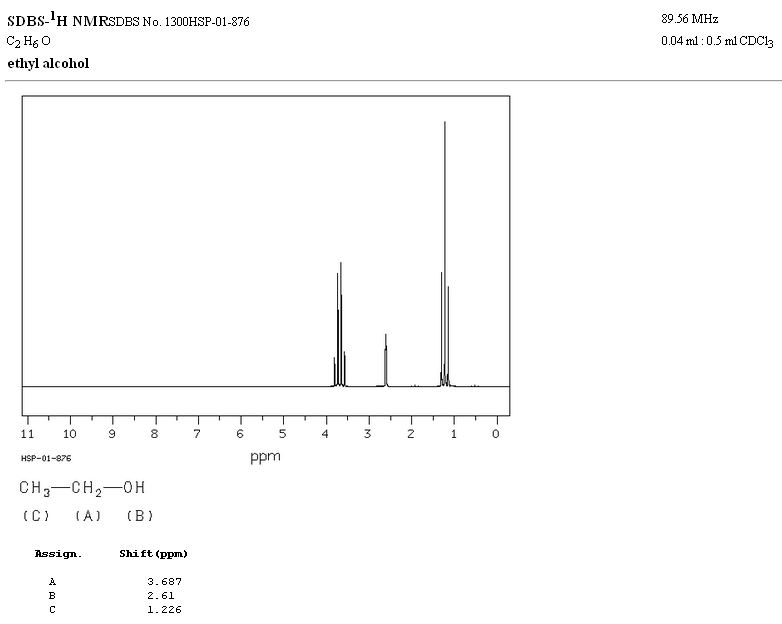
Nello spettro NMR dell'etanolo si osservano tre diversi segnali, dovuti all'esistenza di 3 tipi di idrogeni con differenti ambienti chimici. Gli idrogeni A sono più non schermati di C a causa della presenza di ossigeno (atomo elettronegativo che rimuove la densità elettronica). Anche l'ambiente chimico dell'idrogeno B, direttamente attaccato all'ossigeno, è diverso, risuonando a una frequenza diversa dalle precedenti.

Dettagli

Germán Fernández

Risonanza Magnetica Nucleare (NMR)

Visite: 23691

I segnali nello spettro NMR sono misurati su una scala indipendente dal campo magnetico applicato, chiamato spostamento chimico e rappresentato dalla lettera $\delta$. Indipendentemente dal campo magnetico a cui lavora lo spettrofotometro, i segnali di un composto chimico si ottengono sempre agli stessi valori di $\delta$. \begin{equation} \delta=\frac{\nu_{sample}-\nu_{reference}}{\nu_{reference}}\cdot 10^6 \end{equation} Per definizione è preso come zero della scala di chemical shift il segnale dal tetrametilsilano ($Si(CH_3)_4$). Calcoliamo lo spostamento chimico per $CH_3Br$ sapendo che in un dispositivo a 90 MHz la frequenza di assorbimento avviene a 90 000 237 Hz. \begin{equation} \delta =\frac{90 000 237 - 90 000 000}{ 90 000 000} \cdot 10^{6}=2.63 \end{equation} In uno spettrofotometro che lavora a 300 MHz l'assorbimento avviene a 300 000 790 Hz, ripetendo il calcolo precedente si ottiene lo stesso spostamento chimico. Più idrogeni non schermati escono a spostamenti maggiori: $CH_3Br\rightarrow \delta =2.63$; $CH_2Br_2\rightarrow \delta =$4.90; $CHBr_3\rightarrow\delta = $6,82

Dettagli

Germán Fernández

Risonanza Magnetica Nucleare (NMR)

Visite: 28025

La tabella seguente mostra gli intervalli in cui compaiono i segnali NMR per diversi tipi di idrogeni.

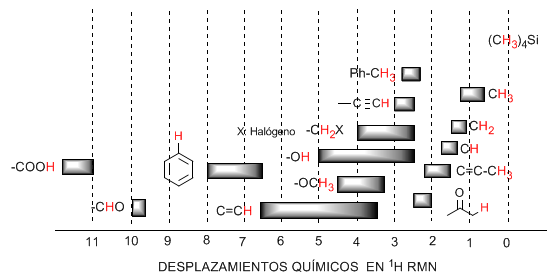
♦ Gli idrogeni localizzati su catene alifatiche presentano valori di $\delta$ prossimi a 1. Aumentano leggermente passando da carboni primari a secondari o terziari.

♦ Gli idrogeni allilici si trovano tra 1,5 e 2,1.

♦ Gli idrogeni alfa rispetto ai carbonili e ai derivati acidi sono compresi tra 2 e 2,5.

♦ Gli idrogeni benzilici tra 2,3 e 2,7.

♦ L'idrogeno degli alchini terminali tra 2,5 e 3.

♦ Idrogeni attaccati ai carboni con alogeni tra 2,5 e 4 a seconda dell'elettronegatività dell'alogeno

♦ Gli idrogeni del gruppo idrossile tra 2,5 e 5. Intervallo molto ampio dovuto alla formazione di legami idrogeno.

♦ Idrogeni con atomi di carbonio legati all'ossigeno di tipo etere tra 3,3 e 4,5.

♦ Idrogeni olefinici tra 3,5 e 6,5.

♦ Idrogeni legati a sistemi aromatici tra 6,5 e 8.

♦ Idrogeno da aldeidi 9.5-10

♦ Idrogeno dal gruppo dell'acido carbossilico superiore a 11.

Dettagli

Germán Fernández

Risonanza Magnetica Nucleare (NMR)

Visite: 14979

I sostituenti elettronegativi rimuovono la densità elettronica, non schermando gli idrogeni e spostano il segnale verso valori \delta$ elevati.

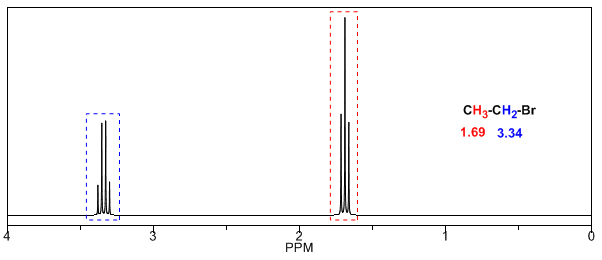
Nella tabella seguente puoi vedere l'influenza di diversi atomi sul segnale degli idrogeni metilici.

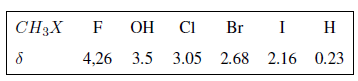
Come si può vedere nella tabella, maggiore è l'elettronegatività del gruppo X, maggiore è lo spostamento chimico.

L'effetto dei gruppi elettronegativi è additivo, maggiore è il numero di gruppi più il protone è non schermato e maggiore è lo spostamento

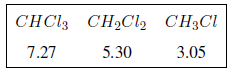
L'effetto induttivo si propaga lungo le catene, diminuendo il suo effetto con la distanza, come si può vedere nella tabella seguente.

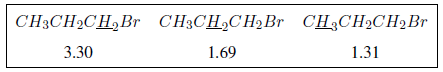
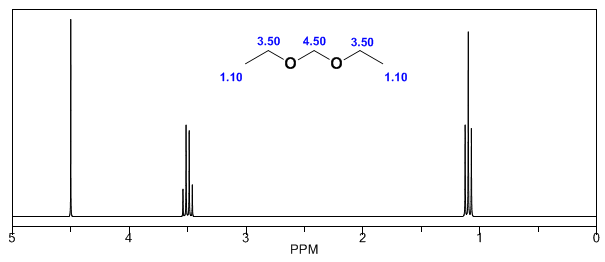
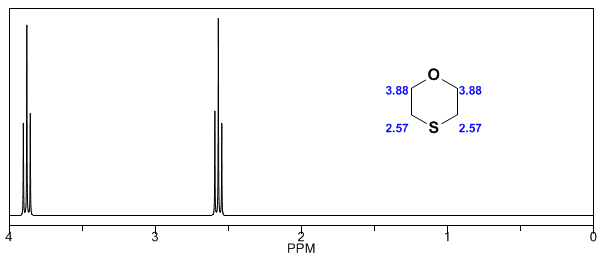
Nei seguenti spettri si possono osservare i suddetti effetti sugli spostamenti chimici.

Dettagli

Germán Fernández

Risonanza Magnetica Nucleare (NMR)

Visite: 22437

I protoni vicini ai doppi legami e agli anelli aromatici sono particolarmente non schermati a causa del campo magnetico indotto dalle correnti elettroniche di questi sistemi. Il campo indotto si somma a quello applicato, producendo uno spostamento maggiore del previsto.

Nell'immagine seguente possiamo vedere la circolazione elettronica (curve in grassetto) e il campo magnetico indotto (linee tratteggiate) per un alchene e un carbonile. Si osservi come nella regione del protone il campo magnetico indotto abbia la stessa direzione e verso di quello applicato.

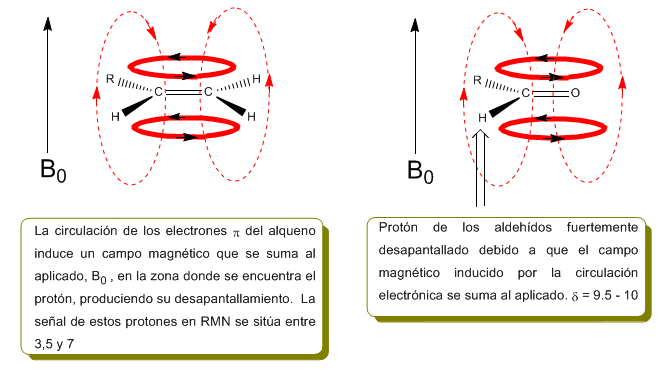
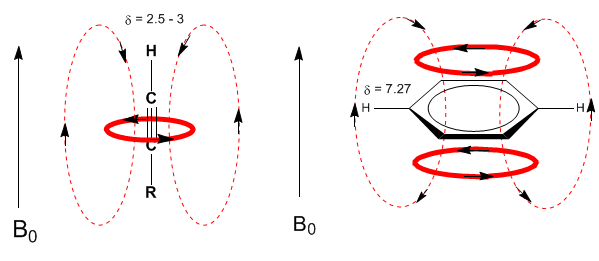
Una situazione simile si osserva nel caso del benzene. Tuttavia, negli alchini, la circolazione elettronica induce un campo magnetico che si oppone a quello applicato nell'area del protone. Gli idrogeni acetilenici sono schermati con segnali nello spettro NMR a bassi offset.

Successivamente, aggiungo alcuni spettri di alcheni, alchini e aromatici.

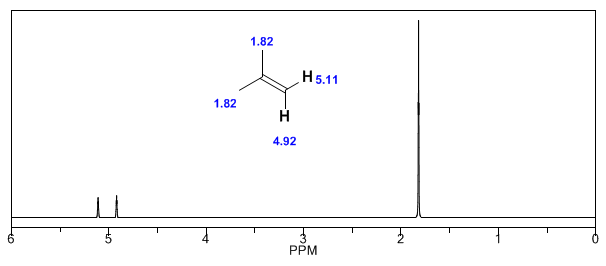
Si osservi come i campi indotti aumentino notevolmente gli spostamenti del protone olefinico, influenzando anche le posizioni alliliche.

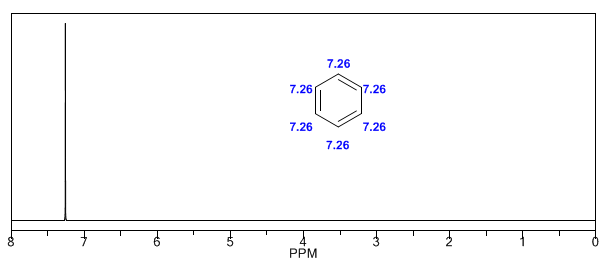
Gli idrogeni aromatici sono fortemente non schermati a causa del campo indotto dalle correnti anulari.

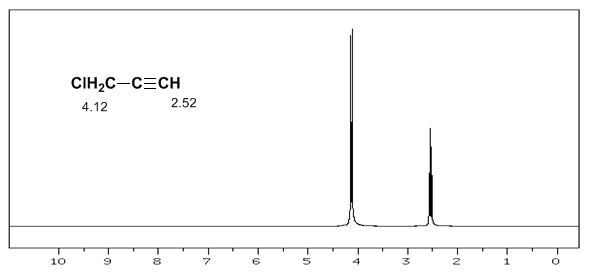
L'idrogeno acetilenico ha un basso spostamento, perché le correnti producono un campo magnetico che si oppone a quello applicato.

Dettagli

Germán Fernández

Risonanza Magnetica Nucleare (NMR)

Visite: 12413

La formazione di legami idrogeno produce valori di spostamento più elevati. La presenza di idrogeni acidi può essere rilevata aggiungendo acqua deuterata, che produce lo scambio di idrogeno acido con deuterio, con la conseguente scomparsa del segnale. \begin{equation} CH_3OH + D_2O \rightleftharpoons CH_3OD + HDO \end{equation} Gli spostamenti acido-idrogeno più comuni nelle molecole organiche sono:

• Acidi carbossilici (RCOOH) $\delta$ = 10 - 12 ppm
• Ammine ($R-NH_2$) $\delta$ = 0,5 - 5 ppm
• Ammidi ($RCONH_2$) $\delta$ = 5-8 ppm
• Alcoli (ROH) $\delta$ = 0,5 - 5 ppm
• Fenoli (Ph-OH) $\delta$ = 4 - 7 ppm

Dettagli

Germán Fernández

Risonanza Magnetica Nucleare (NMR)

Visite: 26122

L'informazione strutturale dell'NMR deriva da due fattori: i diversi spostamenti osservati a seconda dell'ambiente chimico che circonda il protone e l'accoppiamento tra gli spin dei protoni vicini, che produce la scissione dei segnali.

Sebbene alcuni segnali nello spettro siano singoli picchi, è comune trovare segnali composti da più picchi molto ravvicinati, che vengono denominati con la seguente notazione: singoletto (s), doppietto (d), tripletto (t), quadrupletto (c) , quintuplet ( q), sestuplet (sx) e septuplet (sp), i segnali complessi sono designati come multiplet. Il valore di $\delta$ di questi segnali viene assegnato al loro centro, a meno che il multipletto non sia irregolare, nel qual caso viene indicato l'intervallo.

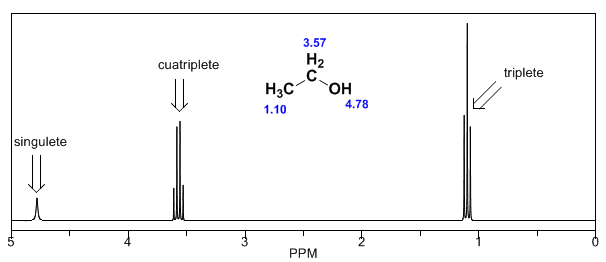
Nello spettro dell'etanolo si può vedere che l'idrogeno idrossilico produce un singoletto, la coppia di idrogeni sul carbonio uno dà origine a un quadruplo, ei tre idrogeni sul carbonio due producono una tripletta.

Spiegazione dell'accoppiamento spin-spin.

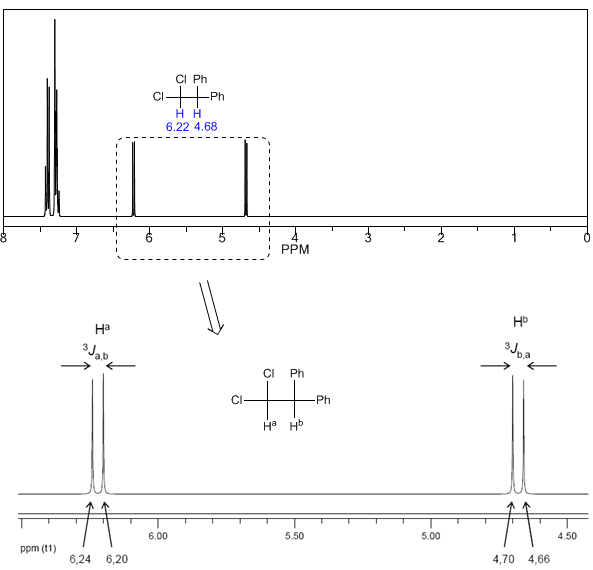
Per comprendere lo sdoppiamento dei segnali dovuto all'accoppiamento spin-spin studieremo lo spettro dell'1,1-dicloro-2,2-difeniletano ($Cl_2CH^{a}CH^{b}Ph_2$).

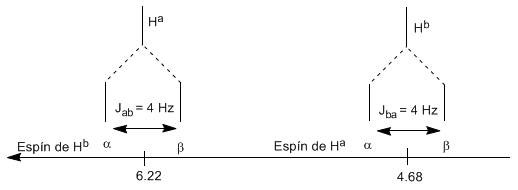
Il protone $H^a$ sottoposto a un campo magnetico $B_0$ produce un segnale a $\delta_a=6.22 ppm$. Tuttavia, il protone $H_b$ genera un piccolo campo magnetico che influenza il protone $H_a$. Circa la metà delle molecole ha il protone $H_b$ allineato con il campo applicato (spin alfa) e l'altra metà lo ha orientato contro il campo (spin beta). Quando $H_b$ ha spin $\alpha$, $H_a$ è soggetto a un campo leggermente più grande e risuona a una frequenza più alta ($\delta$ leggermente più alta). Quando $H_b$ ha spin $\beta$, $H_a$ è soggetta a un campo leggermente più piccolo e risuona a una frequenza inferiore ($\delta$ leggermente inferiore), il che produce la scissione del picco iniziale in due segnali separati da un distanza di 4 Hz, detta costante di accoppiamento (J). Questo stesso ragionamento può essere fatto per il protone $H_b$.

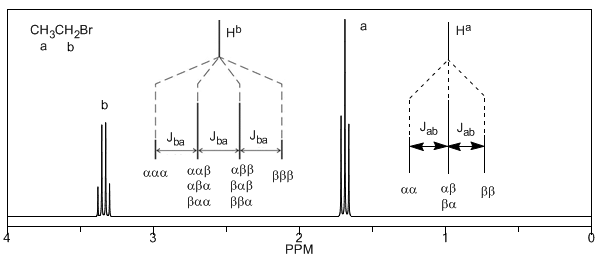
Successivamente, studieremo l'accoppiamento di un idrogeno $H^a$ che ha due idrogeni vicini $H^b$. In questa situazione si osserva la scissione del segnale idrogeno $H^a$ in tre picchi (tripletto), il picco centrale essendo due volte più intenso di quelli estremi. Da parte loro, gli idrogeni $H^b$ si accoppiano con $H^a$ producendo due picchi di uguale intensità (doppietto).

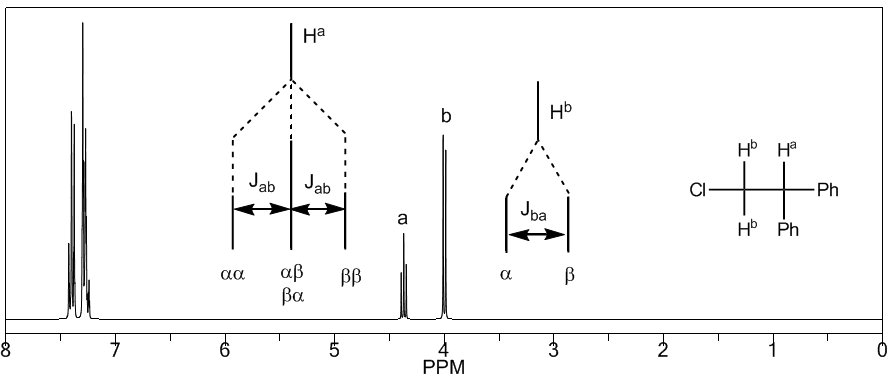
Infine, discuteremo l'accoppiamento di un protone con tre protoni vicini equivalenti. In questo caso si osserva un segnale composto da quattro picchi (quadtripletto). I picchi centrali sono tre volte più intensi dei picchi estremi.

Dettagli

Germán Fernández

Risonanza Magnetica Nucleare (NMR)

Visite: 16540

Dalla discussione precedente si può dedurre che un protone produce un segnale con un numero di picchi un'unità maggiore del numero di idrogeni vicini. Nell'immagine seguente possiamo vedere i picchi prodotti da un idrogeno $H^b$ quando accoppiato con un numero variabile di idrogeni $H^a$

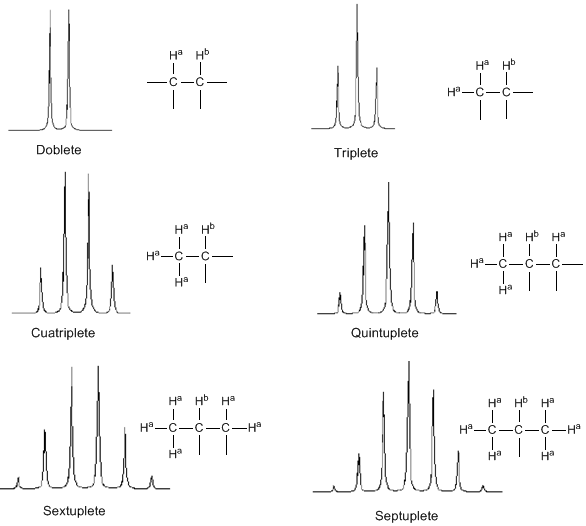
L'intensità dei picchi di un segnale è data dal triangolo di Pascal (Tartaglia)

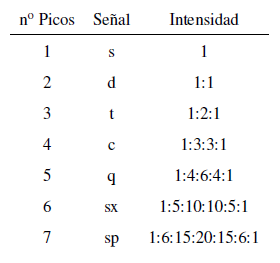
Due considerazioni devono essere prese in considerazione quando si applica la regola N+1:

• Nelle molecole del tipo $A-CH^{a}_2-CH^{b}_2-CH^{a}_2-A$ i protoni $H^b$ appaiono come un quintuplo.
• Nelle molecole del tipo $A-CH_2-CH_2-A$, i quattro protoni sono equivalenti e danno un singoletto.

Dettagli

Germán Fernández

Risonanza Magnetica Nucleare (NMR)

Visite: 11307

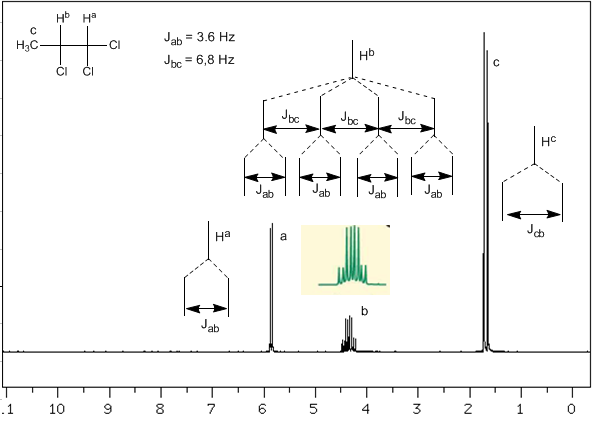
Analizzeremo ora una situazione più complessa in cui i nuclei $H^b$ presentano costanti di accoppiamento diverse con i nuclei vicini $H^c$ e $H^a$. Sapendo che le costanti di accoppiamento tra questi tre nuclei sono $J_{ab}=3.6\;Hz$ e $J_{bc}=6.8\;Hz$, per ottenere il segnale di $H^b$ lo accoppiamo prima con $ H^c$ (massima costante di accoppiamento), che fornisce quattro picchi (regola N+1), che vengono poi accoppiati con $H^a$, ognuno dei quali si divide in due picchi. In totale si ottiene un segnale composto da otto picchi.

Dettagli

Germán Fernández

Risonanza Magnetica Nucleare (NMR)

Visite: 13700

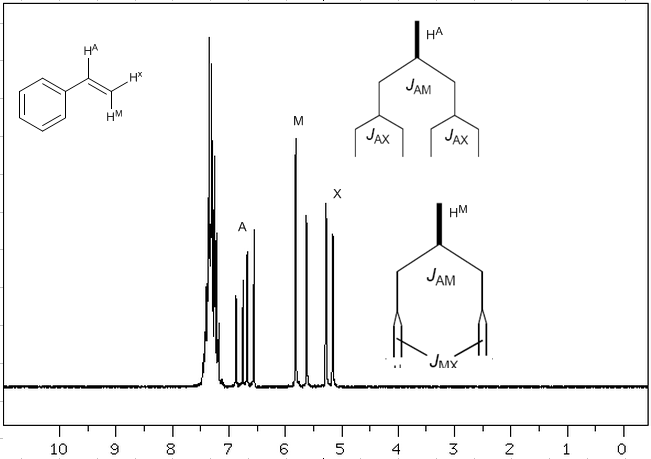
Tenendo conto che l'ordine delle costanti di accoppiamento negli alcheni è $J_{trans}>J_{cis}>J_{geminal}$, gli alberi di accoppiamento per gli idrogeni $H^a$ e $H^M$ sono quelli indicati su lo spettro. Saresti in grado di disegnare l'albero per $H^x$?