In quantum mechanics the magnetic angular momentum in the z direction is given by $L_z=m_I\hbar$. The kernel with $m_I=1/2$ has $L_z=1/2\hbar$, while the kernel with $m_I=-1/2$ has $L_z=-1/2\hbar$. The magnetic moment in this direction is $\mu_z=\gamma L_z$.
These equations allow us to determine the energy of both levels. \begin{equation}\label{ec4} E=-\mu_zB_0=-\gamma m_I\hbar B_0 \end{equation} Now we can calculate the energy difference between the two levels \begin{equation}\label{ec6} \Delta E=-\gamma (-1/2)\hbar B_0 + \gamma 1/2\hbar B_0=\gamma\hbar B_0 \end{equation}
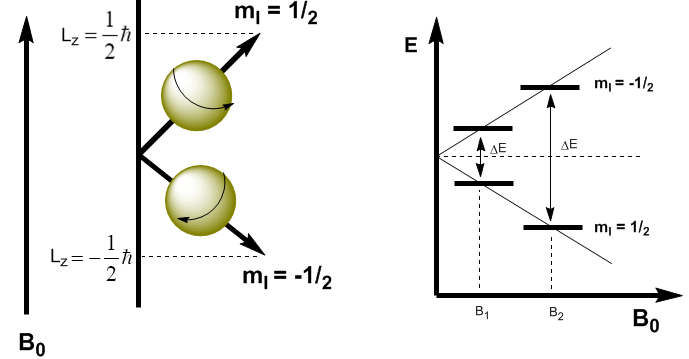
As can be seen in the equation (\ref{ec6}) the energy difference depends on the applied magnetic field. If the magnetic field is low, $\Delta E$ is small and the population difference between the two levels is also small, which causes a sensitivity problem. At high magnetic fields we have a significant separation between levels, which gives rise to a high population difference, obtaining greater sensitivity.