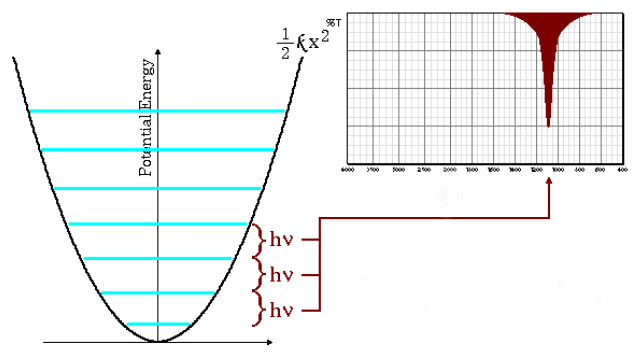
Les vibrations moléculaires peuvent être étudiées avec le modèle d'oscillateur harmonique quantique. L'énergie est donnée par :

\begin{equation}\label{énergie-oscillateur} E_v=\left(v+\frac{1}{2}\right)h\nu \end{equation}

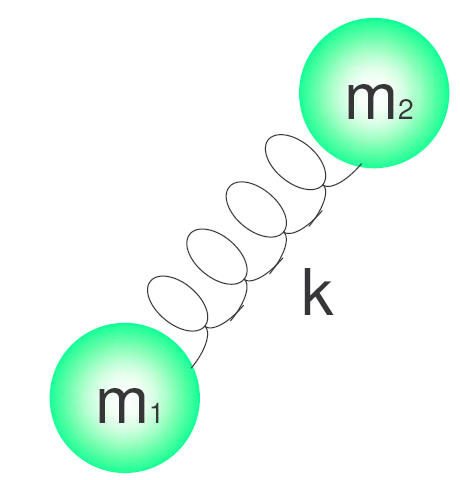
Les différents niveaux d'énergie sont donnés par le nombre quantique v, qui prend les valeurs 0.1.2.3.4.....

h est la constante de Planck et $\nu$ est la fréquence de l'oscillateur qui est donnée par l'expression :\begin{equation} \nu=\frac{1}{2\pi}\sqrt{\frac{k}{\ mu}} \end{equation} Où k est la constante de force du ressort et $\mu$ est la masse réduite du système. $\mu=\frac{m_1m_2}{m_1+m_2}$.

En divisant la fréquence par la vitesse de la lumière, on obtient le nombre d'ondes $\bar{\nu}$ \begin{equation}\label{number-of-waves} \bar{\nu}=\frac{1}{2\pi c}\sqrt{\frac{k}{\mu}} \end{equation} L'étude de l'équation (\ref{number-waves}) nous permettra de prédire à quel nombre d'ondes les liaisons d'une molécule absorbent rayonnement infrarouge. Cette équation n'est applicable qu'aux vibrations de tension.

Hautes fréquences d'absorption

L'équation (\ref{wave-number}) indique que de petites masses réduites (atomes de faible masse) et des constantes de force élevées (liaisons fortes) conduisent à des fréquences élevées. Dans ces conditions, les bandes d'absorption émergent à des nombres d'onde élevés.

Comme on peut le voir sur le graphique, les hautes fréquences donnent lieu à un plus grand espacement entre les niveaux d'énergie.

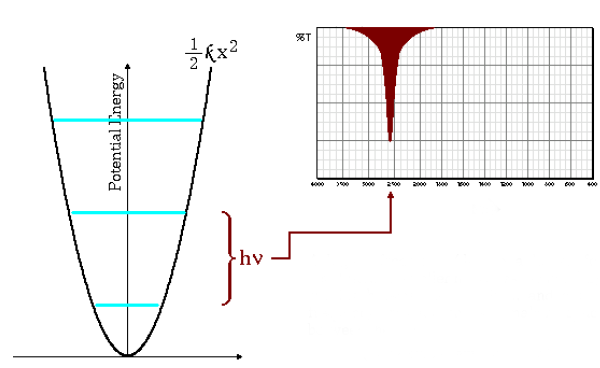
Basses fréquences d'absorption

L'équation (\ref{wave-number}) indique que de grandes petites masses et de petites constantes de force (liaisons faibles) conduisent à des basses fréquences. Dans ces conditions, les bandes d'absorption sortent à de faibles nombres d'onde.

Comme on peut le voir sur le graphique, les basses fréquences donnent lieu à moins d'espacement entre les niveaux d'énergie.