Détails

Germán Fernández

RÉSONANCE MAGNÉTIQUE NUCLÉAIRE (RMN)

Affichages : 13359

Les noyaux atomiques tournent sur eux-mêmes (spin) et présentent un moment angulaire qui est donné par l'expression \begin{equation}\label{ec1} L=\sqrt{I(I+1)}\hbar \end{equation} Moment angulaire dépend du nombre quantique I (nombre quantique de moment angulaire ou spin nucléaire), qui peut prendre des valeurs différentes selon le type de noyau, I=0, 1/2, 1, 3/2, 2, 5/2, 3,.....

Le calcul du nombre quantique de spin d'un noyau se fait en additionnant les spins des protons et des neutrons non appariés. Par exemple, l'hydrogène a I=1/2, car il est composé d'un seul proton.

Les états de spin quantiques autorisés sont donnés par $m_I$, qui prend les valeurs suivantes \begin{equation}\label{ec2} m_I=-I, -I+1, ...., I-1, I \end{equation} Le nombre de valeurs que $m_I$ prend pour une valeur donnée de I est $2I+1$. Ainsi, pour un noyau avec I=1/2 il y a deux états de spin quantique possibles donnés par $m_I=-1/2, 1/2$. Un noyau avec I=1 a trois états de spin quat autorisés $m_I=-1, 0, +1$. En l'absence de champ magnétique, les états quantiques de spin sont dégénérés.

Détails

Germán Fernández

RÉSONANCE MAGNÉTIQUE NUCLÉAIRE (RMN)

Affichages : 13767

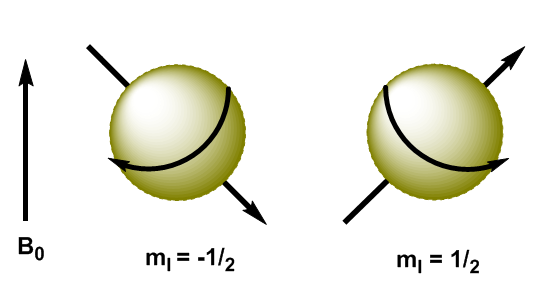
Les noyaux atomiques sont des particules chargées et leur moment cinétique produit un moment magnétique, représenté par $\mu$ \begin{equation}\label{ec3} \mu=\gamma L = \gamma \sqrt{I(I+1)} \hbar \end{equation} où $\gamma$ est la constante gyromanétique, caractéristique de chaque noyau. Lorsque nous appliquons un champ magnétique, $B_0$, aux noyaux avec I=1/2, les moments magnétiques sont orientés de telle manière que les noyaux avec $m_I=1/2$ ont leur moment magnétique aligné avec le champ et le les noyaux avec $ m_I=-1/2$ ont leur moment magnétique opposé au champ appliqué.

Détails

Germán Fernández

RÉSONANCE MAGNÉTIQUE NUCLÉAIRE (RMN)

Affichages : 11129

En mécanique quantique, le moment cinétique magnétique dans la direction z est donné par $L_z=m_I\hbar$. Le noyau avec $m_I=1/2$ a $L_z=1/2\hbar$, tandis que le noyau avec $m_I=-1/2$ a $L_z=-1/2\hbar$. Le moment magnétique dans cette direction est $\mu_z=\gamma L_z$.

Ces équations nous permettent de déterminer l'énergie des deux niveaux. \begin{equation}\label{ec4} E=-\mu_zB_0=-\gamma m_I\hbar B_0 \end{equation} Nous pouvons maintenant calculer la différence d'énergie entre les deux niveaux \begin{equation}\label{ec6} \ Delta E=-\gamma (-1/2)\hbar B_0 + \gamma 1/2\hbar B_0=\gamma\hbar B_0 \end{équation}

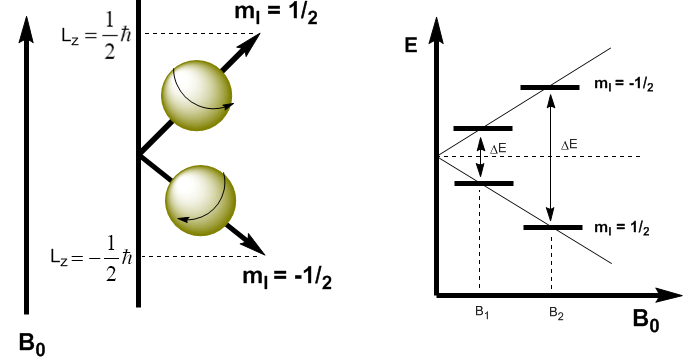
Comme on peut le voir dans l'équation (\ref{ec6}), la différence d'énergie dépend du champ magnétique appliqué. Si le champ magnétique est faible, $\Delta E$ est faible et la différence de population entre les deux niveaux est également faible, ce qui pose un problème de sensibilité. Aux champs magnétiques élevés, nous avons une séparation significative entre les niveaux, ce qui donne lieu à une grande différence de population, obtenant une plus grande sensibilité.

Détails

Germán Fernández

RÉSONANCE MAGNÉTIQUE NUCLÉAIRE (RMN)

Affichages : 13732

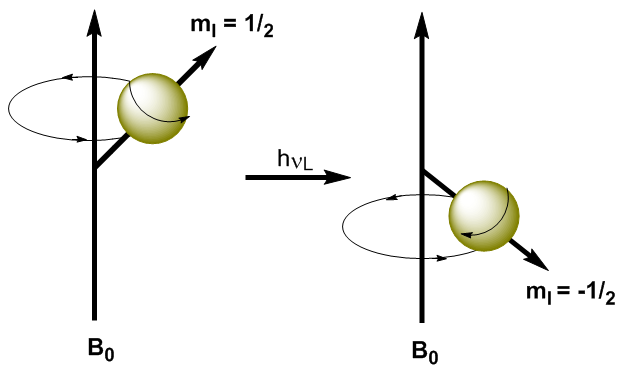
En appliquant un rayonnement électromagnétique de fréquence appropriée (ondes radio), il est possible de faire passer les noyaux du niveau d'énergie inférieur ($m_I=1/2$) au niveau d'énergie supérieur ($m_I=-1/2$). Lorsque le rayonnement électromagnétique et la précession du noyau entrent en résonance, l'absorption se produit. Nous pouvons calculer la fréquence de résonance (fréquence de Larmor) en utilisant l'équation de Planck. \begin{equation}\label{ec7} \Delta E = h\nu_L \end{equation} Remplacer la différence d'énergie par l'équation (\ref{ec7}) \begin{equation}\label{ec8} \gamma\ hbar B_0=h\nu_L \end{equation} Résolution de la fréquence de Larmor \begin{equation}\label{ec10} \nu_L=\frac{\gamma}{2\pi}B_0 \end{equation} Comme on peut le voir dans l'équation (\ref{ec10}), la fréquence à laquelle la transition se produit dépend du champ magnétique appliqué. L'augmentation du champ magnétique produit une augmentation de la différence d'énergie entre les niveaux de spin, de sorte qu'un rayonnement de fréquence plus élevée est nécessaire pour produire la transition.

Détails

Germán Fernández

RÉSONANCE MAGNÉTIQUE NUCLÉAIRE (RMN)

Affichages : 16674

En résonance magnétique, des noyaux avec un moment cinétique de spin différent de zéro sont utilisés, tels que $^1H$ et $^{13}C$. Cependant, les fréquences de résonance ne sont pas les mêmes pour tous les noyaux d'hydrogène ou de carbone, elles dépendent de l'environnement chimique qui entoure chaque noyau. Cela est dû au fait que les électrons entourant chaque noyau génèrent un champ magnétique qui s'oppose à celui appliqué, on dit que les noyaux sont blindés, où $\sigma$ est la constante de blindage. \begin{equation}\label{ec11} B_{eff}=B_0-\sigma B_0=(1-\sigma)B_0 \end{equation} $B_{ef}$ est le champ magnétique net agissant sur le proton ; $B_0$ est le champ magnétique appliqué ; $\sigma$ est la constante de tramage, indépendante du champ appliqué. Dans cette nouvelle situation, avec les noyaux protégés par la densité électronique environnante, la fréquence de résonance devient \begin{equation}\label{ec12} \nu=\frac{\gamma}{2\pi}(1 -\sigma)B_0 \end{equation} Les noyaux avec des environnements chimiques différents ont une constante de criblage différente, générant des signaux différents dans le spectre RMN.

Détails

Germán Fernández

RÉSONANCE MAGNÉTIQUE NUCLÉAIRE (RMN)

Affichages : 22329

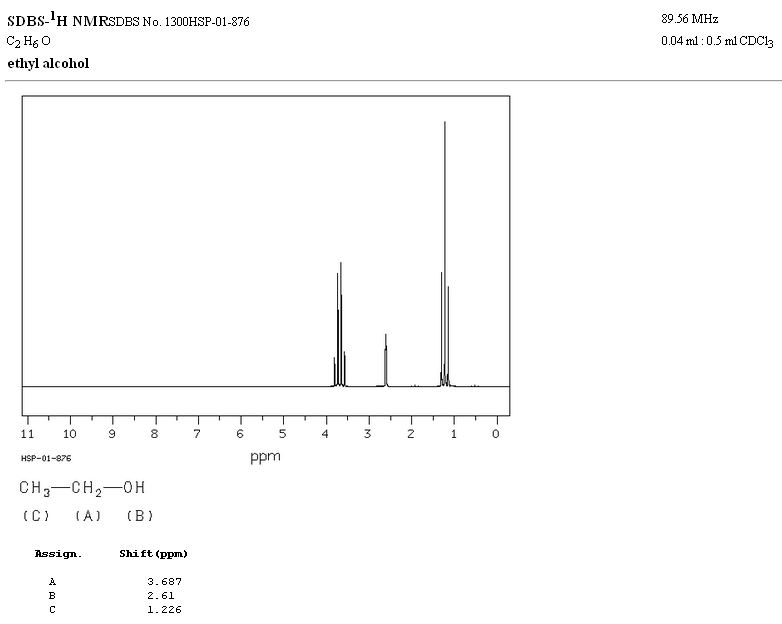
Dans le spectre RMN de l'éthanol, trois signaux différents sont observés, dus à l'existence de 3 types d'hydrogènes avec des environnements chimiques différents. Les hydrogènes A sont plus non blindés que C en raison de la présence d'oxygène (atome électronégatif qui supprime la densité électronique). L'environnement chimique de l'hydrogène B, directement attaché à l'oxygène, est également différent, résonnant à une fréquence différente des précédents.

Détails

Germán Fernández

RÉSONANCE MAGNÉTIQUE NUCLÉAIRE (RMN)

Affichages : 23874

Les signaux du spectre RMN sont mesurés sur une échelle indépendante du champ magnétique appliqué, appelée déplacement chimique et représentée par la lettre $\delta$. Quel que soit le champ magnétique auquel fonctionne le spectrophotomètre, les signaux d'un composé chimique sont toujours obtenus aux mêmes valeurs de $\delta$. \begin{equation} \delta=\frac{\nu_{sample}-\nu_{reference}}{\nu_{reference}}\cdot 10^6 \end{equation} Par définition est pris comme zéro de l'échelle de décaler chimiquement le signal du tétraméthylsilane ($Si(CH_3)_4$). Calculons le déplacement chimique pour $CH_3Br$ sachant que dans un appareil de 90 MHz, la fréquence d'absorption se produit à 90 000 237 Hz. \begin{equation} \delta =\frac{90 000 237 - 90 000 000}{ 90 000 000} \cdot 10^{6}=2.63 \end{equation} Dans un spectrophotomètre travaillant à 300 MHz, l'absorption se produit à 300 000 790 Hz, en répétant le calcul précédent, le même déplacement chimique est obtenu.\ \ Plus les hydrogènes non protégés sortent à déplacements plus importants : $CH_3Br\rightarrow \delta =2,63$ ; $CH_2Br_2\rightarrow \delta =$4.90 ; $CHBr_3\flèchedroite\delta = $6,82

Détails

Germán Fernández

RÉSONANCE MAGNÉTIQUE NUCLÉAIRE (RMN)

Affichages : 28656

Le tableau suivant montre les plages dans lesquelles apparaissent les signaux RMN pour différents types d'hydrogènes.

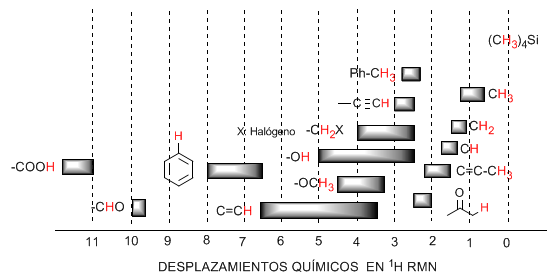
♦ Les hydrogènes situés sur les chaînes aliphatiques présentent des valeurs de $\delta$ proches de 1. Elles augmentent légèrement en passant des carbones primaires aux carbones secondaires ou tertiaires.

♦ Les hydrogènes allyliques sont situés entre 1,5 et 2,1.

♦ Les hydrogènes alpha par rapport aux carbonyles et dérivés acides sont compris entre 2 et 2,5.

♦ Les hydrogènes benzyliques entre 2,3 et 2,7.

♦ L'hydrogène des alcynes terminaux entre 2,5 et 3.

♦ Hydrogènes attachés aux carbones avec des halogènes entre 2,5 et 4 selon l'électronégativité de l'halogène

♦ Les hydrogènes du groupe hydroxyle entre 2,5 et 5. Très large gamme due à la formation de liaisons hydrogène.

♦ Hydrogènes avec des carbones liés à l'oxygène de type éther entre 3,3 et 4,5.

♦ Hydrogènes oléfiniques entre 3,5 et 6,5.

♦ Hydrogènes liés aux systèmes aromatiques entre 6,5 et 8.

♦ Hydrogène des aldéhydes 9,5-10

♦ Hydrogène du groupe acide carboxylique supérieur à 11.

Détails

Germán Fernández

RÉSONANCE MAGNÉTIQUE NUCLÉAIRE (RMN)

Affichages : 15070

Les substituants électronégatifs suppriment la densité électronique, démasquant les hydrogènes et déplacent le signal vers des valeurs \ delta $ élevées.

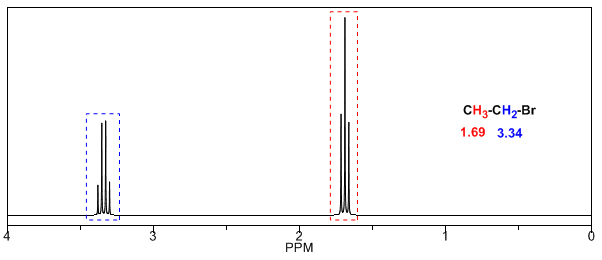
Dans le tableau suivant, vous pouvez voir l'influence de différents atomes sur le signal des hydrogènes de méthyle.

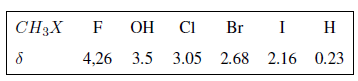
Comme on peut le voir dans le tableau, plus l'électronégativité du groupe X est grande, plus le déplacement chimique est important.

L'effet des groupements électronégatifs est additif, plus le nombre de groupements est élevé plus le proton est non blindé et plus le déplacement est important

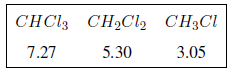
L'effet inductif se propage le long des chaînes, diminuant son effet avec la distance, comme on peut le voir dans le tableau suivant.

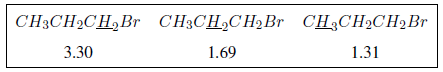
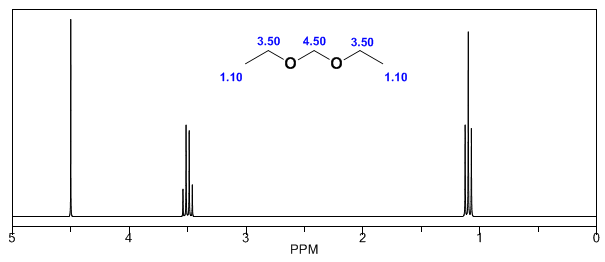
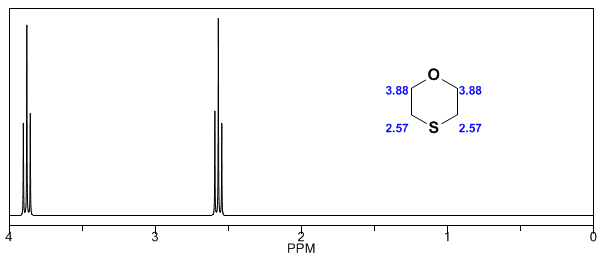
Dans les spectres suivants, les effets susmentionnés sur les déplacements chimiques peuvent être observés.

Détails

Germán Fernández

RÉSONANCE MAGNÉTIQUE NUCLÉAIRE (RMN)

Affichages : 22626

Les protons proches des doubles liaisons et des cycles aromatiques sont notamment non blindés du fait du champ magnétique induit par les courants électroniques de ces systèmes. Le champ induit s'ajoute à celui appliqué, produisant un déplacement plus important que prévu.

Dans l'image suivante on peut voir la circulation électronique (courbes en gras) et le champ magnétique induit (lignes pointillées) pour un alcène et un carbonyle. Observez comment, dans la région du proton, le champ magnétique induit a la même direction et la même direction que celui appliqué.

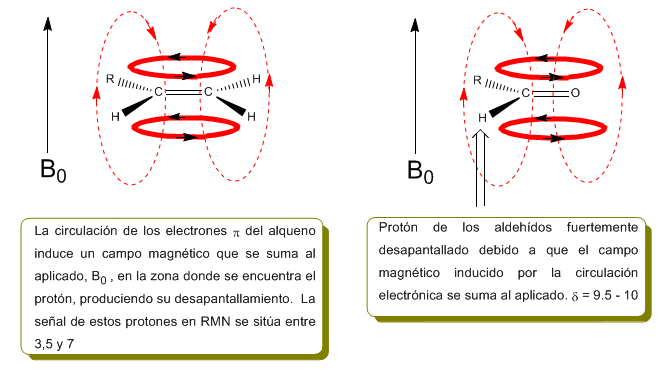
Une situation similaire est observée dans le cas du benzène. Or, dans les alcynes, la circulation électronique induit un champ magnétique opposé à celui appliqué dans le domaine des protons. Les hydrogènes acétyléniques sont protégés par des signaux dans le spectre RMN à faibles décalages.

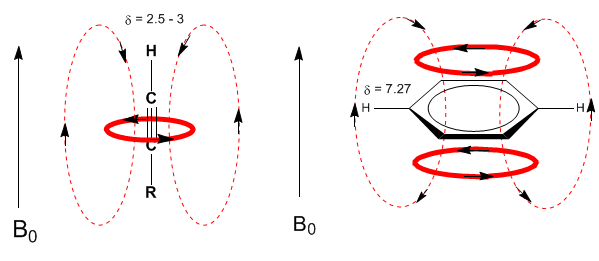
Ensuite, j'ajoute des spectres d'alcènes, d'alcynes et d'aromatiques.

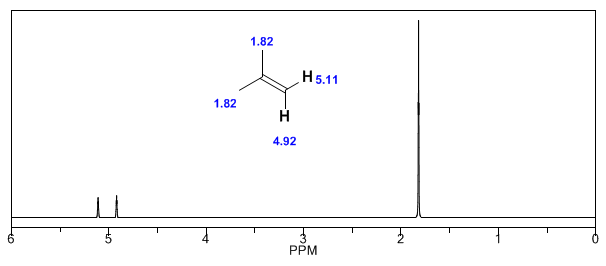
Observez comment les champs induits augmentent considérablement les déplacements du proton oléfinique, les positions allyliques étant également affectées.

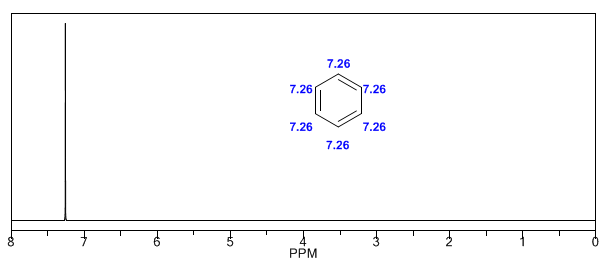
Les hydrogènes aromatiques sont fortement non blindés en raison du champ induit par les courants annulaires.

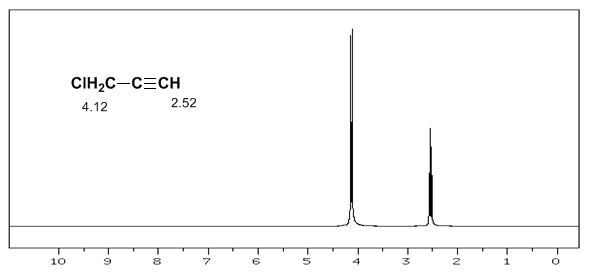
L'hydrogène acétylénique a un faible déplacement, car les courants produisent un champ magnétique qui s'oppose à celui appliqué.

Détails

Germán Fernández

RÉSONANCE MAGNÉTIQUE NUCLÉAIRE (RMN)

Affichages : 12490

La formation de liaisons hydrogène produit des valeurs de déplacement plus élevées. La présence d'hydrogènes acides peut être détectée en ajoutant de l'eau deutérée, ce qui produit l'échange d'hydrogène acide contre du deutérium, avec pour conséquence la disparition du signal. \begin{equation} CH_3OH + D_2O \rightleftharpoons CH_3OD + HDO \end{equation} Les déplacements d'hydrogène acide les plus courants dans les molécules organiques sont :

• Acides carboxyliques (RCOOH) $\delta$ = 10 - 12 ppm
• Amines ($R-NH_2$) $\delta$ = 0,5 - 5 ppm
• Amides ($RCONH_2$) $\delta$ = 5-8 ppm
• Alcools (ROH) $\delta$ = 0,5 - 5 ppm
• Phénols (Ph-OH) $\delta$ = 4 - 7 ppm

Détails

Germán Fernández

RÉSONANCE MAGNÉTIQUE NUCLÉAIRE (RMN)

Affichages : 25910

L'information structurale de la RMN provient de deux facteurs : les différents déplacements observés en fonction de l'environnement chimique qui entoure le proton et le couplage entre les spins des protons proches, qui produit le dédoublement des signaux.

Bien que certains signaux du spectre soient des pics uniques, il est courant de trouver des signaux composés de plusieurs pics très proches, qui sont nommés avec la notation suivante : singulet(s), doublet (d), triplet (t), quadruplet (c) , quintuplet (q), sextuplé (sx) et septuplé (sp), les signaux complexes sont désignés sous le nom de multiplets. La valeur de $\delta$ de ces signaux est affectée à leur centre, sauf si le multiplet est irrégulier, auquel cas l'intervalle est indiqué.

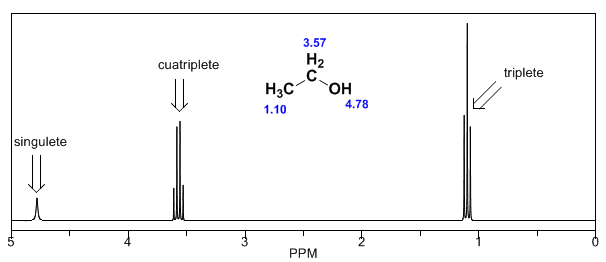
Dans le spectre de l'éthanol, on peut voir que l'hydrogène hydroxyle produit un singulet, la paire d'hydrogènes sur le carbone un donne naissance à un quadruplet et les trois hydrogènes sur le carbone deux produisent un triplet.

Explication du couplage spin-spin.

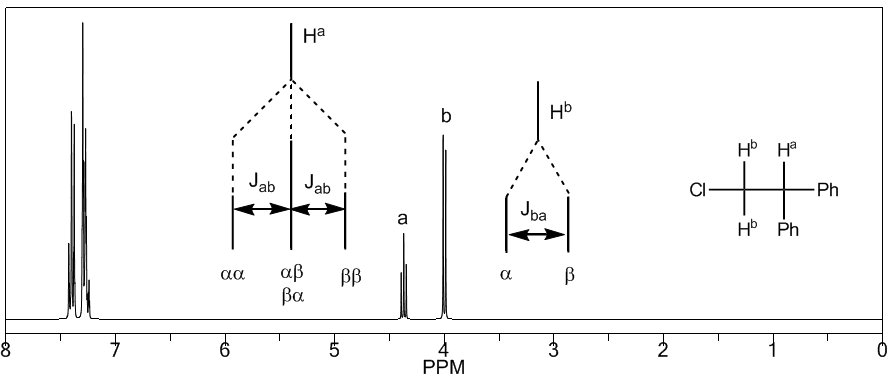
Pour comprendre le dédoublement des signaux dû au couplage spin-spin nous allons étudier le spectre du 1,1-dichloro-2,2-diphényléthane ($Cl_2CH^{a}CH^{b}Ph_2$).

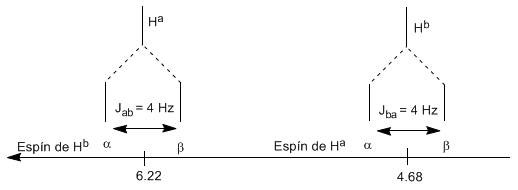
Le proton $H^a$ soumis à un champ magnétique $B_0$ produit un signal à $\delta_a=6,22 ppm$. Cependant, le proton $H_b$ génère un petit champ magnétique qui affecte le proton $H_a$. Environ la moitié des molécules ont le proton $H_b$ aligné avec le champ appliqué (spin alpha) et l'autre moitié l'ont orienté contre le champ (spin bêta). Lorsque $H_b$ a un spin $\alpha$, $H_a$ est soumis à un champ légèrement plus grand et résonne à une fréquence plus élevée ($\delta$ légèrement plus élevée). Lorsque $H_b$ a un spin $\beta$, $H_a$ est soumis à un champ légèrement plus petit et résonne à une fréquence plus basse ($\delta$ légèrement plus basse), ce qui produit le dédoublement du pic initial en deux signaux séparés par un distance de 4 Hz, appelée constante de couplage (J). Ce même raisonnement peut être fait pour le proton $H_b$.

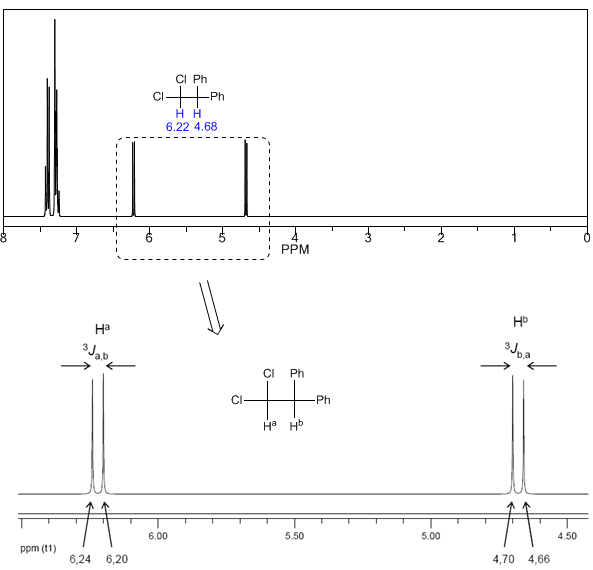
Ensuite, nous étudierons le couplage d'un hydrogène $H^a$ ayant deux hydrogènes $H^b$ voisins. Dans cette situation, on observe le dédoublement du signal hydrogène $H^a$ en trois pics (triplet), le pic central étant deux fois plus intense que les extrêmes. De leur côté, les hydrogènes $H^b$ se couplent avec $H^a$ produisant deux pics d'égale intensité (doublet).

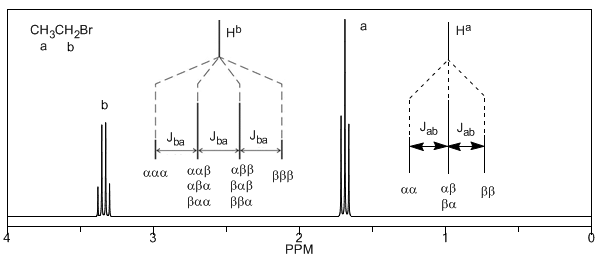
Enfin, nous aborderons le couplage d'un proton avec trois protons voisins équivalents. Dans ce cas, on observe un signal composé de quatre pics (quadtriplet). Les pics centraux sont trois fois plus intenses que les pics extrêmes.

Détails

Germán Fernández

RÉSONANCE MAGNÉTIQUE NUCLÉAIRE (RMN)

Affichages : 16458

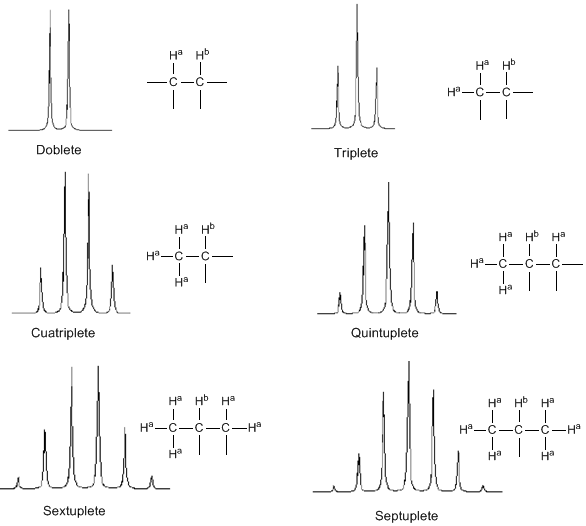
De la discussion ci-dessus, on peut déduire qu'un proton produit un signal avec un nombre de pics supérieur d'une unité au nombre d'hydrogènes voisins. Dans l'image suivante, nous pouvons voir les pics produits par un hydrogène $H^b$ lorsqu'il est couplé avec un certain nombre d'hydrogènes variables $H^a$

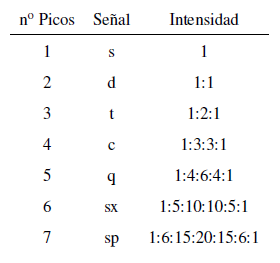
L'intensité des pics d'un signal est donnée par le triangle de Pascal (Tartaglia)

Deux considérations doivent être prises en compte lors de l'application de la règle N+1 :

• Dans les molécules de type $A-CH2^{a}-CH2}^{b}-CH2}^{a}-A$, les protons $H^b$ apparaissent comme un quintuplet.
• Dans les molécules de type $A-CH_2-CH_2-A$, les quatre protons sont équivalents et donnent un singulet.

Détails

Germán Fernández

RÉSONANCE MAGNÉTIQUE NUCLÉAIRE (RMN)

Affichages : 11343

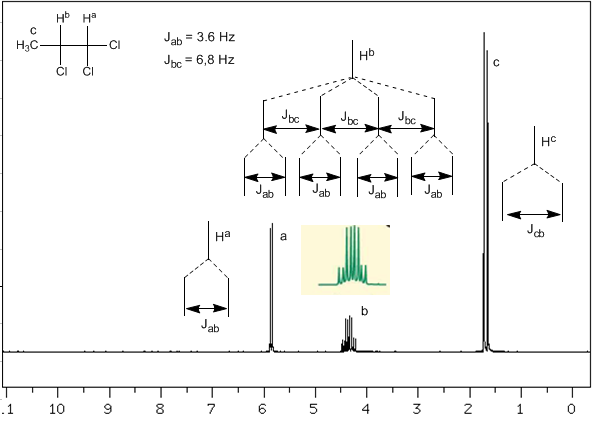
Nous allons maintenant analyser une situation plus complexe dans laquelle les noyaux $H^b$ présentent des constantes de couplage différentes avec les noyaux voisins $H^c$ et $H^a$. Sachant que les constantes de couplage entre ces trois noyaux sont $J_{ab}=3.6\;Hz$ et $J_{bc}=6.8\;Hz$, pour obtenir le signal de $H^b$ on le couple d'abord avec $ H^c$ (plus grande constante de couplage), donnant quatre pics (règle N+1), qui sont ensuite couplés avec $H^a$, chacun se divisant en deux pics. Au total, un signal composé de huit pics est obtenu.

Détails

Germán Fernández

RÉSONANCE MAGNÉTIQUE NUCLÉAIRE (RMN)

Affichages : 14077

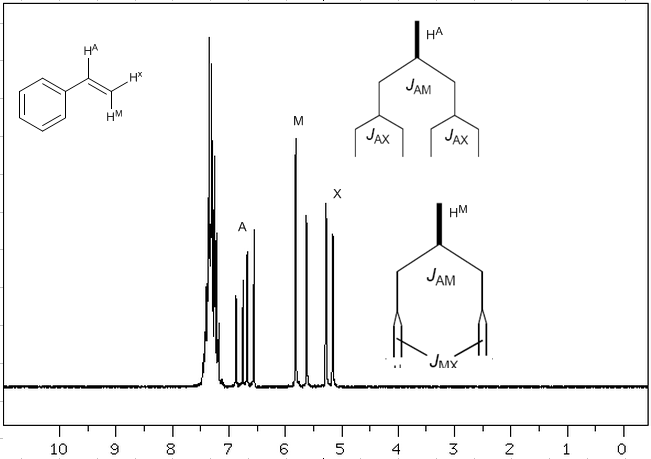
En tenant compte du fait que l'ordre des constantes de couplage dans les alcènes est $J_{trans}>J_{cis}>J_{geminal}$, les arbres de couplage pour les hydrogènes $H^a$ et $H^M$ sont ceux indiqués sur le spectre. Seriez-vous capable de dessiner l'arbre pour $H^x$ ?