Molekulare Schwingungen können mit dem Modell des harmonischen Quantenoszillators untersucht werden. Die Energie ergibt sich aus:

\begin{equation}\label{Energie-Oszillator} E_v=\left(v+\frac{1}{2}\right)h\nu \end{equation}

Die unterschiedlichen Energieniveaus sind durch die Quantenzahl v gegeben, die Werte von 0,1,2,3,4 annimmt.....

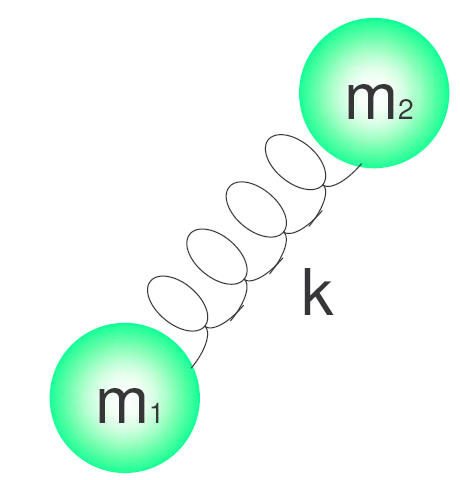
h ist die Plancksche Konstante und $\nu$ ist die Frequenz des Oszillators, die durch den Ausdruck gegeben ist:\begin{equation} \nu=\frac{1}{2\pi}\sqrt{\frac{k}{\ mu}} \end{equation} Dabei ist k die Kraftkonstante der Feder und $\mu$ die reduzierte Masse des Systems. $\mu=\frac{m_1m_2}{m_1+m_2}$.

Teilt man die Frequenz durch die Lichtgeschwindigkeit, erhält man die Wellenzahl $\bar{\nu}$ \begin{equation}\label{number-of-waves} \bar{\nu}=\frac{1}{2\pi c}\sqrt{\frac{k}{\mu}} \end{equation} Das Studium der Gleichung (\ref{number-waves}) erlaubt uns vorherzusagen, bei welcher Wellenzahl die Bindungen eines Moleküls absorbieren Infrarotstrahlung . Diese Gleichung gilt nur für Zugschwingungen.

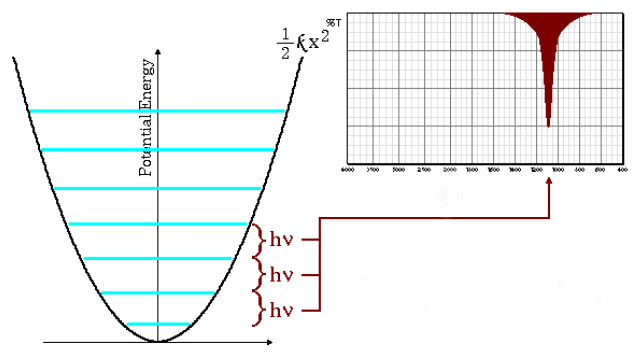
Hohe Absorptionsfrequenzen

Die Gleichung (\ref{Wellenzahl}) zeigt, dass kleine reduzierte Massen (atome mit geringer Masse) und große Kraftkonstanten (starke Bindungen) zu hohen Frequenzen führen. Unter diesen Bedingungen entstehen die Absorptionsbanden bei hohen Wellenzahlen.

Wie in der Grafik zu sehen ist, führen hohe Frequenzen zu einem größeren Abstand zwischen den Energieniveaus.

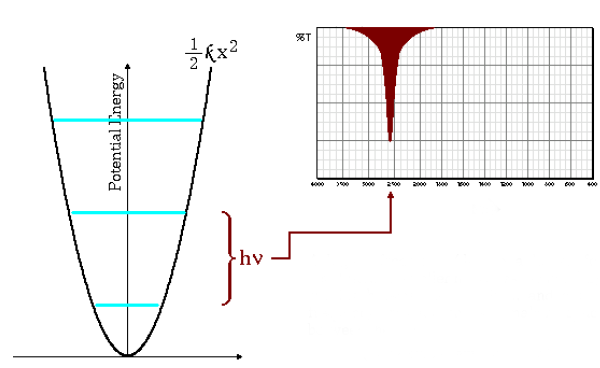
Niedrige Absorptionsfrequenzen

Die Gleichung (\ref{Wellenzahl}) zeigt, dass große kleine Massen und kleine Kraftkonstanten (schwache Bindungen) zu niedrigen Frequenzen führen. Unter diesen Bedingungen treten die Absorptionsbanden bei niedrigen Wellenzahlen auf.

Wie in der Grafik zu sehen ist, führen niedrige Frequenzen zu einem geringeren Abstand zwischen den Energieniveaus.