Detail

Germán Fernández

RESONANSI MAGNETIK NUKLIR (NMR)

Dilihat: 13380

Inti atom berotasi (berputar) dan menghadirkan momentum sudut yang diberikan oleh ekspresi \begin{equation}\label{ec1} L=\sqrt{I(I+1)}\hbar \end{equation} Momentum sudut tergantung pada bilangan kuantum I (bilangan kuantum momentum sudut atau putaran nuklir), yang dapat mengambil nilai yang berbeda tergantung pada jenis inti, I=0, 1/2, 1, 3/2, 2, 5/2, 3,.....

Perhitungan bilangan kuantum spin untuk inti dilakukan dengan menjumlahkan spin proton dan neutron yang tidak berpasangan. Misalnya, hidrogen memiliki I=1/2, karena hanya terdiri dari satu proton.

Status spin kuantum yang diizinkan diberikan oleh $m_I$, yang mengambil nilai berikut \begin{equation}\label{ec2} m_I=-I, -I+1, ...., I-1, I \end{equation} dua kemungkinan keadaan spin kuantum yang diberikan oleh $m_I=-1/2, 1/2$. Inti dengan I=1 memiliki tiga status spin quat yang diizinkan $m_I=-1, 0, +1$. Dengan tidak adanya medan magnet, keadaan spin kuantum merosot.

Detail

Germán Fernández

RESONANSI MAGNETIK NUKLIR (NMR)

Dilihat: 13857

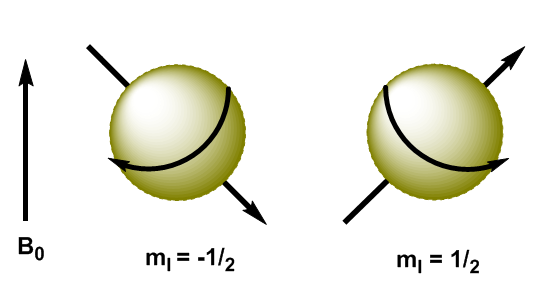
Inti atom adalah partikel bermuatan dan momentum sudutnya menghasilkan momentum magnet, dilambangkan dengan $\mu$ \begin{equation}\label{ec3} \mu=\gamma L = \gamma \sqrt{I(I+1)} \hbar \end{equation} di mana $\gamma$ adalah konstanta gyromanetic, karakteristik dari setiap nukleus. Ketika kita menerapkan medan magnet, $B_0$, ke inti dengan I=1/2, momen magnet diorientasikan sedemikian rupa sehingga inti dengan $m_I=1/2$ memiliki momen magnetnya sejajar dengan medan dan inti dengan $ m_I=-1/2$ memiliki momen magnet yang berlawanan dengan medan yang diterapkan.

Detail

Germán Fernández

RESONANSI MAGNETIK NUKLIR (NMR)

Dilihat: 11170

Dalam mekanika kuantum momentum sudut magnetik dalam arah z diberikan oleh $L_z=m_I\hbar$. Kernel dengan $m_I=1/2$ memiliki $L_z=1/2\hbar$, sedangkan kernel dengan $m_I=-1/2$ memiliki $L_z=-1/2\hbar$. Momen magnetik pada arah ini adalah $\mu_z=\gamma L_z$.

Persamaan ini memungkinkan kita untuk menentukan energi dari kedua tingkat. \begin{equation}\label{ec4} E=-\mu_zB_0=-\gamma m_I\hbar B_0 \end{equation} Sekarang kita dapat menghitung perbedaan energi antara dua tingkat \begin{equation}\label{ec6} \ Delta E=-\gamma (-1/2)\hbar B_0 + \gamma 1/2\hbar B_0=\gamma\hbar B_0 \end{equation}

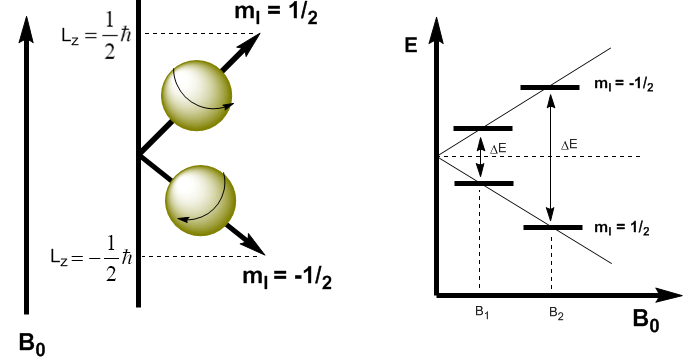
Seperti dapat dilihat pada persamaan (\ref{ec6}) perbedaan energi bergantung pada medan magnet yang diterapkan. Jika medan magnet rendah, $\Delta E$ kecil dan perbedaan populasi antara dua level juga kecil, yang menyebabkan masalah sensitivitas. Pada medan magnet tinggi kami memiliki pemisahan yang signifikan antara level, yang menimbulkan perbedaan populasi yang tinggi, memperoleh sensitivitas yang lebih besar.

Detail

Germán Fernández

RESONANSI MAGNETIK NUKLIR (NMR)

Dilihat: 13386

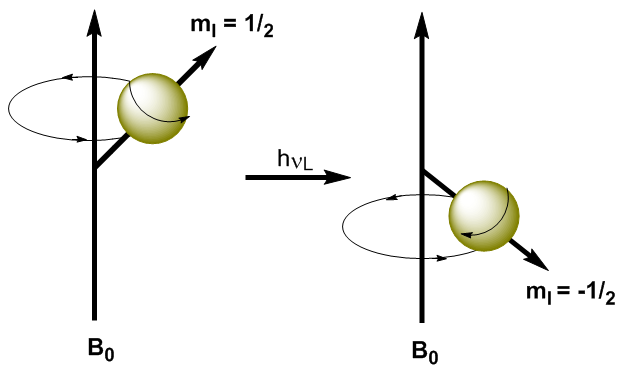
Dengan menerapkan radiasi elektromagnetik dengan frekuensi yang sesuai (gelombang radio), dimungkinkan untuk mempromosikan inti dari tingkat energi yang lebih rendah ($m_I=1/2$) ke tingkat energi yang lebih tinggi ($m_I=-1/2$). Ketika radiasi elektromagnetik dan presesi inti memasuki resonansi, terjadi penyerapan. Kita dapat menghitung frekuensi resonansi (frekuensi Larmor) menggunakan persamaan Planck. \begin{equation}\label{ec7} \Delta E = h\nu_L \end{equation} Mengganti perbedaan energi dengan persamaan (\ref{ec7}) \begin{equation}\label{ec8} \gamma\ hbar B_0=h\nu_L \end{equation} Menyelesaikan Larmor Frequency \begin{equation}\label{ec10} \nu_L=\frac{\gamma}{2\pi}B_0 \end{equation} Seperti yang terlihat dalam persamaan (\ref{ec10}) frekuensi terjadinya transisi bergantung pada medan magnet yang diterapkan. Peningkatan medan magnet menghasilkan peningkatan perbedaan energi antara tingkat putaran, sehingga diperlukan radiasi frekuensi yang lebih tinggi untuk menghasilkan transisi.

Detail

Germán Fernández

RESONANSI MAGNETIK NUKLIR (NMR)

Dilihat: 16641

Dalam resonansi magnetik, inti dengan momentum sudut spin selain nol digunakan, seperti $^1H$ dan $^{13}C$. Namun, frekuensi resonansi tidak sama untuk semua inti hidrogen atau karbon, mereka bergantung pada lingkungan kimiawi yang mengelilingi setiap inti. Hal ini disebabkan oleh fakta bahwa elektron yang mengelilingi setiap nukleus menghasilkan medan magnet yang berlawanan dengan medan magnet yang diterapkan, dikatakan bahwa nukleus terlindung, di mana $\sigma$ adalah konstanta perisai. \begin{equation}\label{ec11} B_{eff}=B_0-\sigma B_0=(1-\sigma)B_0 \end{equation} $B_{ef}$ adalah medan magnet total yang bekerja pada proton; $B_0$ adalah medan magnet yang diterapkan; $\sigma$ adalah konstanta penyaringan, terlepas dari bidang yang diterapkan. Dalam situasi baru ini, dengan inti terlindung oleh kerapatan elektron di sekitarnya, frekuensi resonansi menjadi \begin{equation}\label{ec12} \nu=\frac{\gamma}{2\pi}(1 -\sigma)B_0 \end{equation} Inti dengan lingkungan kimia yang berbeda memiliki konstanta penyaring yang berbeda, menghasilkan sinyal yang berbeda dalam spektrum NMR.

Detail

Germán Fernández

RESONANSI MAGNETIK NUKLIR (NMR)

Dilihat: 21700

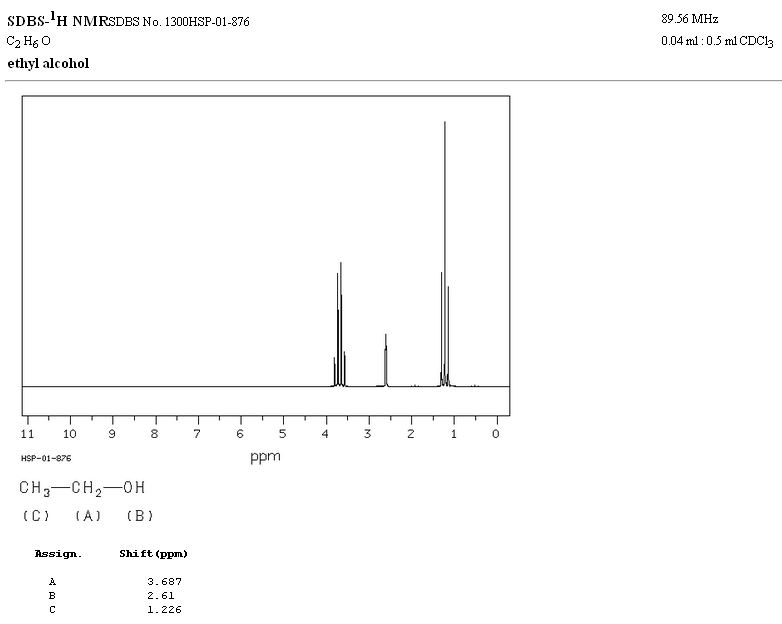
Dalam spektrum NMR etanol, tiga sinyal berbeda diamati, karena adanya 3 jenis hidrogen dengan lingkungan kimia yang berbeda. Hidrogen A lebih tidak terlindungi daripada C karena adanya oksigen (atom elektronegatif yang menghilangkan kerapatan elektron). Lingkungan kimiawi hidrogen B, yang langsung menempel pada oksigen, juga berbeda, beresonansi pada frekuensi yang berbeda dari frekuensi sebelumnya.

Detail

Germán Fernández

RESONANSI MAGNETIK NUKLIR (NMR)

Dilihat: 23822

Sinyal dalam spektrum NMR diukur pada skala independen dari medan magnet yang diterapkan, yang disebut pergeseran kimia dan diwakili oleh huruf $\delta$. Terlepas dari medan magnet tempat spektrofotometer bekerja, sinyal senyawa kimia selalu diperoleh dengan nilai $\delta$ yang sama. \begin{equation} \delta=\frac{\nu_{sample}-\nu_{reference}}{\nu_{reference}}\cdot 10^6 \end{equation} Menurut definisi diambil nol dari skala kimiawi menggeser sinyal dari tetramethylsilane ($Si(CH_3)_4$). Mari hitung pergeseran kimia untuk $CH_3Br$ dengan mengetahui bahwa dalam perangkat 90 MHz frekuensi penyerapan terjadi pada 90 000 237 Hz.\begin{equation} \delta =\frac{90 000 237 - 90 000 000}{ 90 000 000} \cdot 10^{6}=2.63 \end{equation} Dalam spektrofotometer yang bekerja pada 300 MHz, penyerapan terjadi pada 300 000 790 Hz, mengulangi perhitungan sebelumnya diperoleh pergeseran kimia yang sama.\ \ Semakin banyak hidrogen yang tidak terlindung keluar pada perpindahan yang lebih besar: $CH_3Br\rightarrow \delta =2.63$; $CH_2Br_2\rightarrow \delta =$4,90; $CHBr_3\panah kanan \delta = $6,82

Detail

Germán Fernández

RESONANSI MAGNETIK NUKLIR (NMR)

Dilihat: 28449

Tabel berikut menunjukkan rentang di mana sinyal NMR muncul untuk berbagai jenis hidrogen.

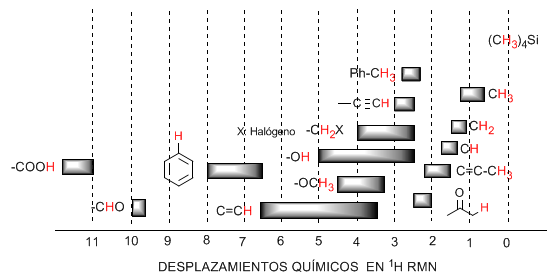
♦ Hidrogen yang terletak pada rantai alifatik menunjukkan nilai $\delta$ mendekati 1. Hidrogen meningkat sedikit ketika berpindah dari karbon primer ke karbon sekunder atau tersier.

♦ Hidrogen alilik terletak antara 1,5 dan 2,1.

♦ Hidrogen alfa sehubungan dengan karbonil dan turunan asam adalah antara 2 dan 2,5.

♦ Hidrogen benzilik antara 2,3 dan 2,7.

♦ Hidrogen alkin terminal antara 2,5 dan 3.

♦ Hidrogen terikat pada karbon dengan halogen antara 2,5 dan 4 bergantung pada keelektronegatifan halogen

♦ Hidrogen dari gugus hidroksil antara 2,5 dan 5. Kisaran yang sangat luas karena pembentukan ikatan hidrogen.

♦ Hidrogen dengan karbon terikat oksigen tipe eter antara 3,3 dan 4,5.

♦ Hidrogen olefin antara 3,5 dan 6,5.

♦ Hidrogen terikat pada sistem aromatik antara 6,5 dan 8.

♦ Hidrogen dari aldehida 9.5-10

♦ Hidrogen dari gugus asam karboksilat di atas 11.

Detail

Germán Fernández

RESONANSI MAGNETIK NUKLIR (NMR)

Dilihat: 15233

Substituen elektronegatif menghilangkan kerapatan elektron, membuka pelindung hidrogen, dan menggeser sinyal ke nilai \delta$ tinggi.

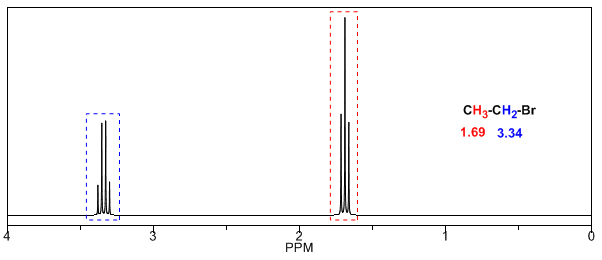
Pada tabel berikut Anda dapat melihat pengaruh atom yang berbeda pada sinyal metil hidrogen.

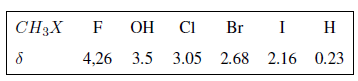
Seperti dapat dilihat pada tabel, semakin besar keelektronegatifan golongan X, semakin besar pula pergeseran kimianya.

Pengaruh gugus elektronegatif bersifat aditif, semakin besar jumlah gugus maka proton semakin tidak terlindung dan perpindahan semakin besar

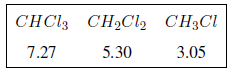
Efek induktif menyebar sepanjang rantai, mengurangi efeknya dengan jarak, seperti yang dapat dilihat pada tabel berikut.

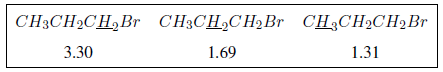
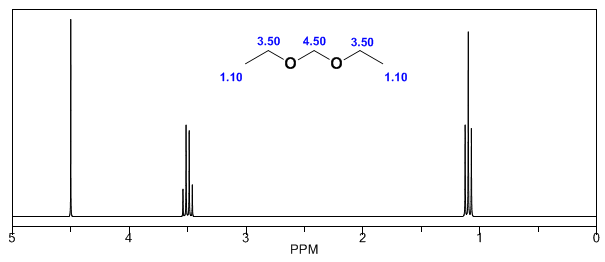
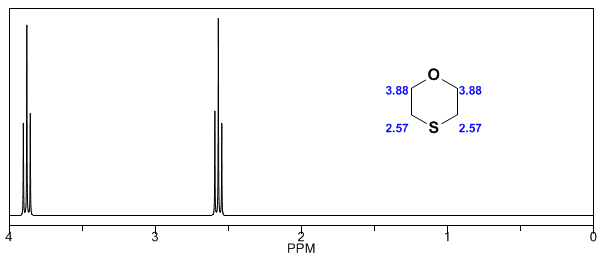
Dalam spektrum berikut, efek pergeseran kimia yang disebutkan di atas dapat diamati.

Detail

Germán Fernández

RESONANSI MAGNETIK NUKLIR (NMR)

Dilihat: 21840

Proton yang dekat dengan ikatan rangkap dan cincin aromatik secara khusus tidak terlindung karena medan magnet yang diinduksi oleh arus elektronik dari sistem ini. Medan terinduksi ditambahkan ke yang diterapkan, menghasilkan perpindahan yang lebih besar dari yang diharapkan.

Pada gambar berikut kita dapat melihat sirkulasi elektronik (kurva dicetak tebal) dan medan magnet induksi (garis putus-putus) untuk alkena dan karbonil. Amati bagaimana di wilayah proton medan magnet yang diinduksi memiliki arah dan arah yang sama dengan yang diterapkan.

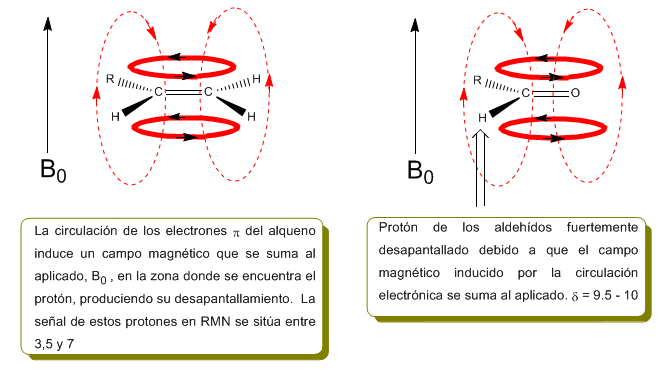
Situasi serupa diamati dalam kasus benzena. Namun, dalam alkuna, sirkulasi elektronik menginduksi medan magnet yang berlawanan dengan yang diterapkan di area proton. Hidrogen asetilen terlindung dengan sinyal dalam spektrum NMR pada offset rendah.

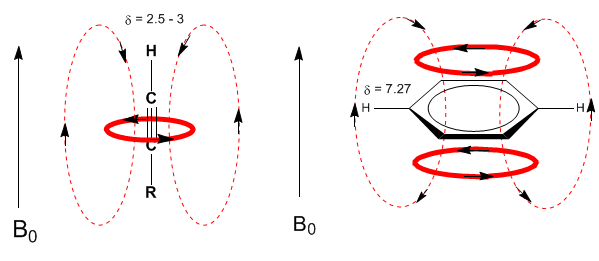
Selanjutnya, saya menambahkan beberapa spektrum alkena, alkin, dan aromatik.

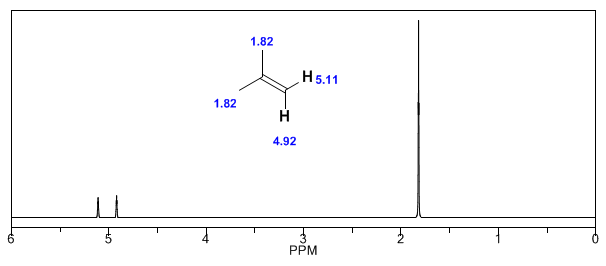
Amati bagaimana medan terinduksi sangat meningkatkan perpindahan proton olefin, posisi alilik juga terpengaruh.

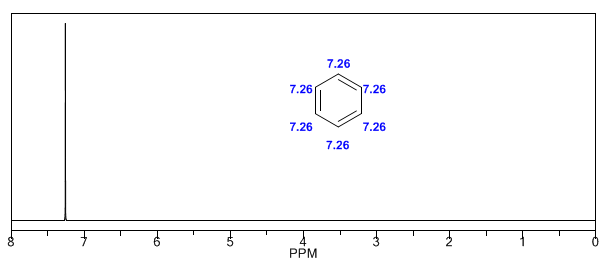
Hidrogen aromatik sangat tidak terlindungi karena medan yang diinduksi oleh arus cincin.

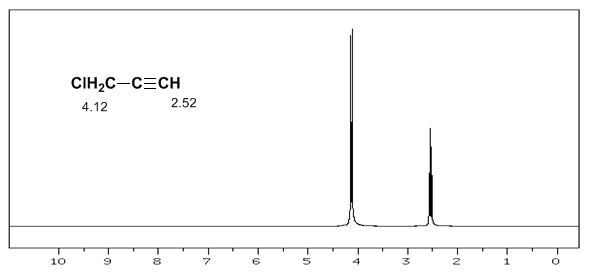
Hidrogen asetilena memiliki perpindahan yang rendah, karena arus menghasilkan medan magnet yang berlawanan dengan yang diterapkan.

Detail

Germán Fernández

RESONANSI MAGNETIK NUKLIR (NMR)

Dilihat: 12657

Pembentukan ikatan hidrogen menghasilkan nilai perpindahan yang lebih tinggi. Kehadiran hidrogen asam dapat dideteksi dengan menambahkan air deuterasi, yang menghasilkan pertukaran hidrogen asam dengan deuterium, dengan konsekuensi hilangnya sinyal. \begin{equation} CH_3OH + D_2O \rightleftharpoons CH_3OD + HDO \end{equation} Pergeseran hidrogen asam yang paling umum dalam molekul organik adalah:

• Asam karboksilat (RCOOH) $\delta$ = 10 - 12 ppm
• Amina ($R-NH_2$) $\delta$ = 0,5 - 5 ppm
• Amida ($RCONH_2$) $\delta$ = 5-8 ppm
• Alkohol (ROH) $\delta$ = 0,5 - 5 ppm
• Fenol (Ph-OH) $\delta$ = 4 - 7 ppm

Detail

Germán Fernández

RESONANSI MAGNETIK NUKLIR (NMR)

Dilihat: 26126

Informasi struktural NMR berasal dari dua faktor: perpindahan berbeda yang diamati tergantung pada lingkungan kimia yang mengelilingi proton dan kopling antara putaran proton terdekat, yang menghasilkan pemisahan sinyal.

Meskipun beberapa sinyal dalam spektrum adalah puncak tunggal, adalah umum untuk menemukan sinyal yang terdiri dari beberapa puncak yang sangat dekat, yang diberi nama dengan notasi berikut: singlet (s), doublet (d), triplet (t), quadruplet (c) , kuintuplet ( q), sextuplet (sx) dan septuplet (sp), sinyal kompleks ditetapkan sebagai multiplet. Nilai $\delta$ dari sinyal-sinyal ini ditetapkan ke pusatnya, kecuali multipletnya tidak beraturan, dalam hal ini intervalnya ditunjukkan.

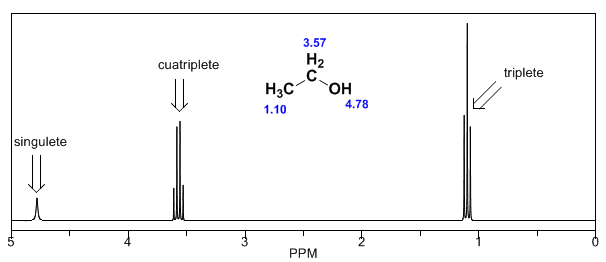
Dalam spektrum etanol dapat dilihat bahwa hidrogen hidroksil menghasilkan singlet, pasangan hidrogen pada karbon satu menimbulkan quadruplet, dan tiga hidrogen pada karbon dua menghasilkan triplet.

Penjelasan spin-spin kopling.

Untuk memahami pemisahan sinyal akibat kopling spin-spin, kita akan mempelajari spektrum 1,1-dikloro-2,2-difeniletana ($Cl_2CH^{a}CH^{b}Ph_2$).

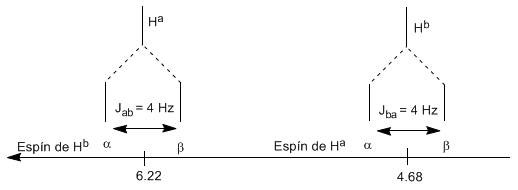
Proton $H^a$ mengalami medan magnet $B_0$ menghasilkan sinyal pada $\delta_a=6.22 ppm$. Namun, proton $H_b$ menghasilkan medan magnet kecil yang mempengaruhi proton $H_a$. Kira-kira setengah dari molekul memiliki proton $H_b$ sejajar dengan medan yang diterapkan (putaran alfa) dan separuh lainnya berorientasi terhadap medan (putaran beta). Ketika $H_b$ telah berputar $\alpha$, $H_a$ dikenai bidang yang sedikit lebih besar dan beresonansi pada frekuensi yang lebih tinggi ($\delta$ sedikit lebih tinggi). Ketika $H_b$ telah berputar $\beta$, $H_a$ dikenai bidang yang sedikit lebih kecil dan beresonansi pada frekuensi yang lebih rendah ($\delta$ sedikit lebih rendah), yang menghasilkan pemisahan puncak awal menjadi dua sinyal yang dipisahkan oleh a jarak 4 Hz, disebut konstanta kopling (J). Alasan yang sama dapat dilakukan untuk proton $H_b$.

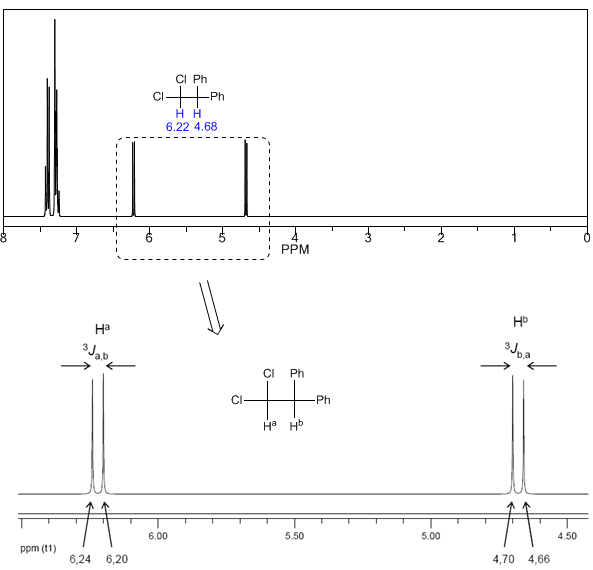
Selanjutnya, kita akan mempelajari kopling hidrogen $H^a$ yang memiliki dua hidrogen tetangga $H^b$. Dalam situasi ini, pemisahan sinyal hidrogen $H^a$ menjadi tiga puncak (triplet) diamati, puncak pusat menjadi dua kali lebih kuat dari yang ekstrim. Untuk bagian mereka, hidrogen $H^b$ berpasangan dengan $H^a$ menghasilkan dua puncak dengan intensitas yang sama (doublet).

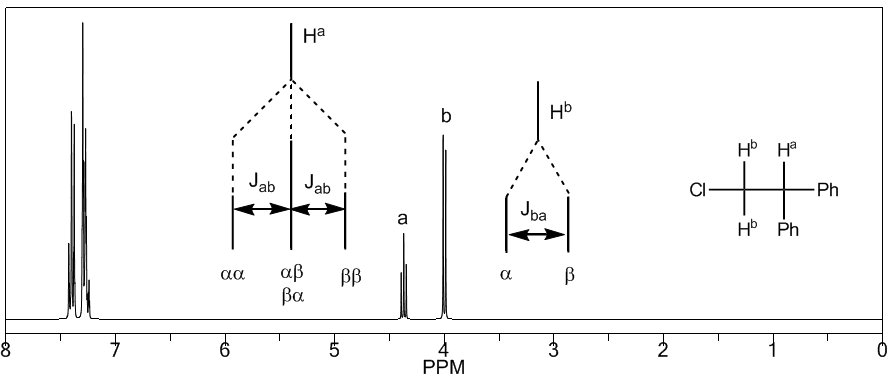
Terakhir, kita akan membahas kopling proton dengan tiga proton tetangga yang ekuivalen. Dalam hal ini, sinyal yang terdiri dari empat puncak (quadtriplet) diamati. Puncak pusat tiga kali lebih kuat dari puncak ekstrim.

Detail

Germán Fernández

RESONANSI MAGNETIK NUKLIR (NMR)

Dilihat: 16513

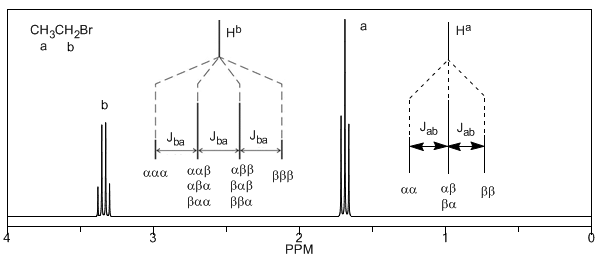
Dari pembahasan di atas dapat ditarik kesimpulan bahwa sebuah proton menghasilkan sinyal dengan jumlah puncak satu unit lebih besar dari jumlah hidrogen tetangganya. Pada gambar berikut kita dapat melihat puncak yang dihasilkan oleh hidrogen $H^b$ ketika digabungkan dengan sejumlah hidrogen variabel $H^a$

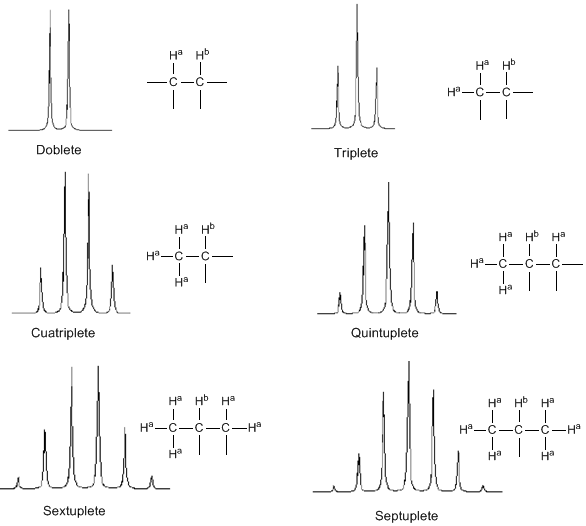
Intensitas puncak sinyal diberikan oleh segitiga Pascal (Tartaglia)

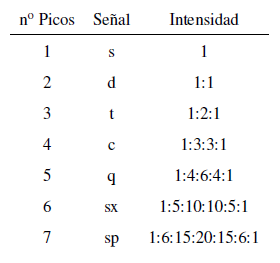
Dua pertimbangan harus diperhitungkan saat menerapkan aturan N+1:

• Dalam molekul tipe $A-CH2^{a}-CH2}^{b}-CH2}^{a}-A$ proton $H^b$ muncul sebagai kuintuplet.
• Dalam molekul tipe $A-CH_2-CH_2-A$, keempat protonnya ekuivalen dan menghasilkan singlet.

Detail

Germán Fernández

RESONANSI MAGNETIK NUKLIR (NMR)

Dilihat: 11340

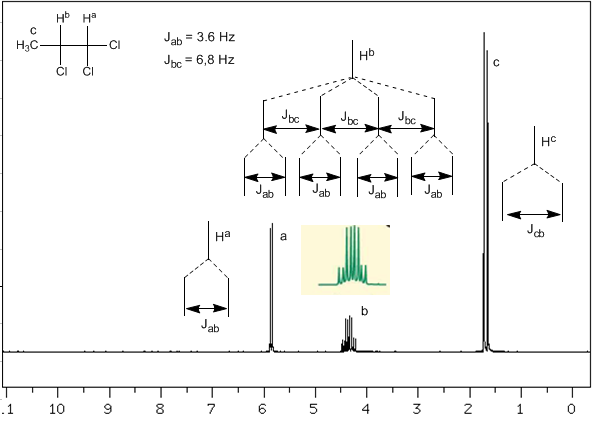
Sekarang kita akan menganalisis situasi yang lebih kompleks di mana inti $H^b$ menyajikan konstanta penggandengan yang berbeda dengan inti tetangga $H^c$ dan $H^a$. Mengetahui bahwa konstanta kopling antara ketiga inti ini adalah $J_{ab}=3.6\;Hz$ dan $J_{bc}=6.8\;Hz$, untuk mendapatkan sinyal $H^b$ pertama kita pasangkan dengan $ H^c$ (konstanta kopling terbesar), memberikan empat puncak (aturan N+1), yang kemudian digabungkan dengan $H^a$, masing-masing membelah menjadi dua puncak. Secara total, sinyal yang terdiri dari delapan puncak diperoleh.

Detail

Germán Fernández

RESONANSI MAGNETIK NUKLIR (NMR)

Dilihat: 13620

Mempertimbangkan bahwa urutan konstanta penggandengan dalam alkena adalah $J_{trans}>J_{cis}>J_{geminal}$, pohon penggandengan untuk hidrogen $H^a$ dan $H^M$ ditunjukkan pada spektrum. Apakah Anda dapat menggambar pohon untuk $H^x$?