Detalhes

Germán Fernández

RESSONÂNCIA MAGNÉTICA NUCLEAR (NMR)

Acessos: 13513

Os núcleos atômicos giram sobre si mesmos (spin) e apresentam um momento angular que é dado pela expressão \begin{equation}\label{ec1} L=\sqrt{I(I+1)}\hbar \end{equation} Momento angular depende do número quântico I (número quântico do momento angular ou spin nuclear), que pode assumir diferentes valores dependendo do tipo de núcleo, I=0, 1/2, 1, 3/2, 2, 5/2, 3,.....

O cálculo do número quântico de spin para um núcleo é feito adicionando os spins de prótons e nêutrons desemparelhados. Por exemplo, o hidrogênio tem I=1/2, pois é formado por apenas um próton.

Os estados de spin quântico permitidos são dados por $m_I$, que assume os seguintes valores \begin{equation} m_I=-I, -I+1, ...., I-1, I \end{equation} O número de valores que $m_I$ leva para um determinado valor de I é $2I+1$. Assim, para um núcleo com I=1/2 existem dois possíveis estados de spin quântico dados por $m_I=-1/2, 1/2$. Um núcleo com I=1 tem três estados quat de spin permitidos $m_I=-1, 0, +1$. Na ausência de um campo magnético, os estados quânticos de spin são degenerados.

Detalhes

Germán Fernández

RESSONÂNCIA MAGNÉTICA NUCLEAR (NMR)

Acessos: 13746

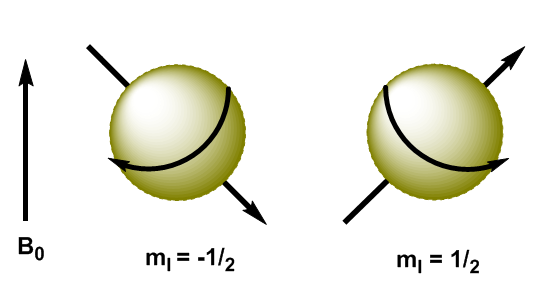
Núcleos atômicos são partículas carregadas e seu momento angular produz momento magnético, representado por $\mu$ \begin{equation}\label{ec3} \mu=\gamma L = \gamma \sqrt{I(I+1)} \hbar \end{equation} onde $\gamma$ é a constante giromanética, característica de cada núcleo. Quando aplicamos um campo magnético, $B_0$, a núcleos com I=1/2, os momentos magnéticos são orientados de forma que os núcleos com $m_I=1/2$ tenham seu momento magnético alinhado com o campo e o núcleos com $ m_I=-1/2$ têm seu momento magnético oposto ao campo aplicado.

Detalhes

Germán Fernández

RESSONÂNCIA MAGNÉTICA NUCLEAR (NMR)

Acessos: 11095

Na mecânica quântica, o momento angular magnético na direção z é dado por $L_z=m_I\hbar$. O kernel com $m_I=1/2$ tem $L_z=1/2\hbar$, enquanto o kernel com $m_I=-1/2$ tem $L_z=-1/2\hbar$. O momento magnético nesta direção é $\mu_z=\gamma L_z$.

Estas equações nos permitem determinar a energia de ambos os níveis. \begin{equation}\label{ec4} E=-\mu_zB_0=-\gamma m_I\hbar B_0 \end{equation} Agora podemos calcular a diferença de energia entre os dois níveis \begin{equation}\label{ec6} \ Delta E=-\gamma (-1/2)\hbar B_0 + \gamma 1/2\hbar B_0=\gamma\hbar B_0 \end{equação}

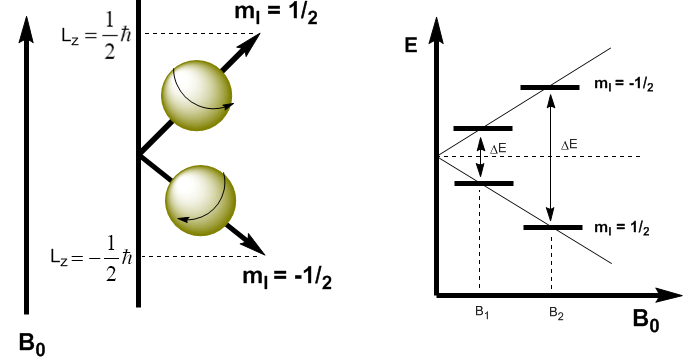
Como pode ser visto na equação (\ref{ec6}) a diferença de energia depende do campo magnético aplicado. Se o campo magnético for baixo, $\Delta E$ é pequeno e a diferença populacional entre os dois níveis também é pequena, o que causa um problema de sensibilidade. Em campos magnéticos altos temos uma separação significativa entre os níveis, o que dá origem a uma alta diferença populacional, obtendo maior sensibilidade.

Detalhes

Germán Fernández

RESSONÂNCIA MAGNÉTICA NUCLEAR (NMR)

Acessos: 13575

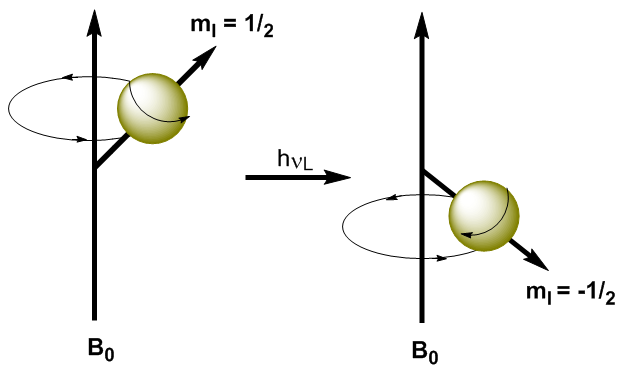
Aplicando radiação eletromagnética de frequência adequada (ondas de rádio) é possível promover os núcleos do nível de energia mais baixo ($m_I=1/2$) para o nível de energia mais alto ($m_I=-1/2$). Quando a radiação eletromagnética e a precessão do núcleo entram em ressonância, ocorre a absorção. Podemos calcular a frequência de ressonância (frequência de Larmor) usando a equação de Planck. \begin{equation}\label{ec7} \Delta E = h\nu_L \end{equation} Substituindo a diferença de energia pela equação (\ref{ec7}) \begin{equation}\label{ec8} \gamma\ hbar B_0=h\nu_L \end{equation} Resolvendo a frequência de Larmor \begin{equation}\label{ec10} \nu_L=\frac{\gamma}{2\pi}B_0 \end{equation} Como pode ser visto na equação (\ref{ec10}) a frequência na qual a transição ocorre depende do campo magnético aplicado. O aumento do campo magnético produz um aumento na diferença de energia entre os níveis de spin, de modo que uma radiação de maior frequência é necessária para produzir a transição.

Detalhes

Germán Fernández

RESSONÂNCIA MAGNÉTICA NUCLEAR (NMR)

Acessos: 16861

Na Ressonância Magnética, são utilizados núcleos com momento angular de spin diferente de zero, como $^1H$ e $^{13}C$. No entanto, as frequências de ressonância não são as mesmas para todos os núcleos de hidrogênio ou carbono, elas dependem do ambiente químico que envolve cada núcleo. Isso se deve ao fato de que os elétrons ao redor de cada núcleo geram um campo magnético oposto ao aplicado, diz-se que os núcleos são blindados, onde $\sigma$ é a constante de blindagem. \begin{equation}\label{ec11} B_{eff}=B_0-\sigma B_0=(1-\sigma)B_0 \end{equation} $B_{ef}$ é o campo magnético resultante atuando no próton; $B_0$ é o campo magnético aplicado; $\sigma$ é a constante de triagem, independente do campo aplicado. Nessa nova situação, com os núcleos blindados pela densidade eletrônica circundante, a frequência de ressonância torna-se \begin{equation}\label{ec12} \nu=\frac{\gamma}{2\pi}(1 -\sigma)B_0 \end{equation} Núcleos com diferentes ambientes químicos possuem diferentes constantes de triagem, gerando diferentes sinais no espectro de RMN.

Detalhes

Germán Fernández

RESSONÂNCIA MAGNÉTICA NUCLEAR (NMR)

Acessos: 21974

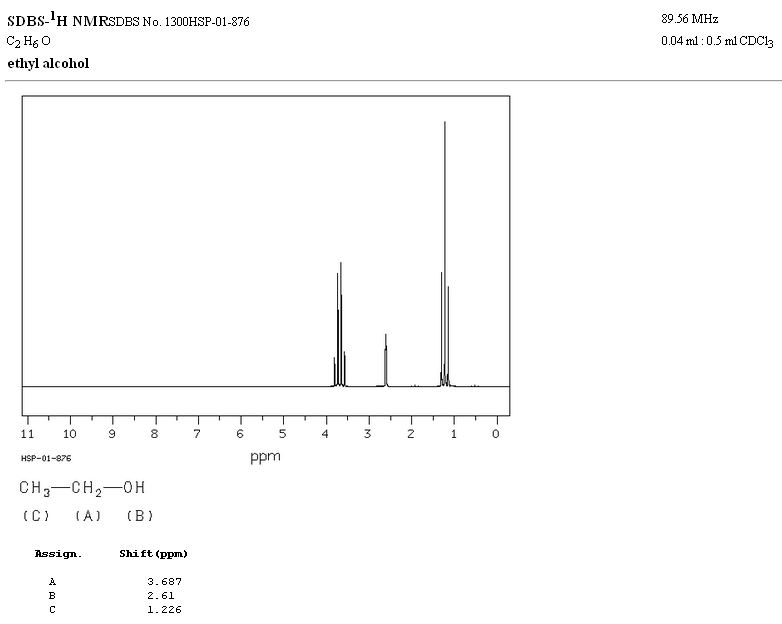
No espectro de RMN do etanol, três sinais diferentes são observados, devido à existência de 3 tipos de hidrogênios com ambientes químicos diferentes. Os hidrogênios A são mais desprotegidos do que C devido à presença de oxigênio (átomo eletronegativo que remove a densidade de elétrons). O ambiente químico do hidrogênio B, diretamente ligado ao oxigênio, também é diferente, ressoando em uma frequência diferente das anteriores.

Detalhes

Germán Fernández

RESSONÂNCIA MAGNÉTICA NUCLEAR (NMR)

Acessos: 23762

Os sinais no espectro de RMN são medidos em uma escala independente do campo magnético aplicado, chamada de deslocamento químico e representada pela letra $\delta$. Independentemente do campo magnético em que o espectrofotômetro trabalha, os sinais de um composto químico são sempre obtidos nos mesmos valores de $\delta$. \begin{equation} \delta=\frac{\nu_{amostra}-\nu_{referência}}{\nu_{referência}}\cdot 10^6 \end{equation} Por definição é tomado como zero da escala de desvio químico do sinal do tetrametilsilano ($Si(CH_3)_4$). Vamos calcular o deslocamento químico para $CH_3Br$ sabendo que em um aparelho de 90 MHz a frequência de absorção ocorre em 90 000 237 Hz. \begin{equation} \delta =\frac{90 000 237 - 90 000 000}{ 90 000 000} \cdot 10^{6}=2.63 \end{equation} Em um espectrofotômetro trabalhando a 300 MHz a absorção ocorre a 300 000 790 Hz, repetindo o cálculo anterior obtém-se o mesmo deslocamento químico.\ \ Quanto mais hidrogênios não blindados saem a deslocamentos maiores: $CH_3Br\rightarrow \delta =2.63$; $CH_2Br_2\rightarrow \delta =$4,90; $CHBr_3\rightarrow \delta = $6,82

Detalhes

Germán Fernández

RESSONÂNCIA MAGNÉTICA NUCLEAR (NMR)

Acessos: 28084

A tabela a seguir mostra as faixas nas quais os sinais de NMR aparecem para diferentes tipos de hidrogênios.

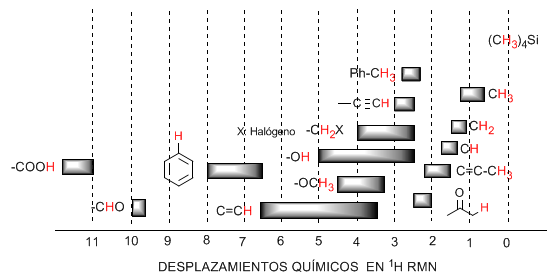
♦ Os hidrogênios localizados nas cadeias alifáticas apresentam valores de $\delta$ próximos de 1. Aumentam ligeiramente ao passar de carbonos primários para carbonos secundários ou terciários.

♦ Os hidrogênios alílicos estão localizados entre 1,5 e 2,1.

♦ Hidrogênios alfa em relação a carbonilas e derivados de ácidos estão entre 2 e 2,5.

♦ Os hidrogênios benzílicos entre 2,3 e 2,7.

♦ O hidrogênio dos alcinos terminais entre 2,5 e 3.

♦ Hidrogênios ligados a carbonos com halogênios entre 2,5 e 4, dependendo da eletronegatividade do halogênio

♦ Os hidrogênios do grupo hidroxila entre 2,5 e 5. Gama muito ampla devido à formação de pontes de hidrogênio.

♦ Hidrogênios com carbonos ligados a oxigênio do tipo éter entre 3,3 e 4,5.

♦ Hidrogênios olefínicos entre 3,5 e 6,5.

♦ Hidrogênios ligados a sistemas aromáticos entre 6,5 e 8.

♦ Hidrogênio de aldeídos 9,5-10

♦ Hidrogênio do grupo ácido carboxílico acima de 11.

Detalhes

Germán Fernández

RESSONÂNCIA MAGNÉTICA NUCLEAR (NMR)

Acessos: 15093

Substituintes eletronegativos removem a densidade eletrônica, desprotegindo os hidrogênios, e deslocam o sinal para valores altos de \delta$.

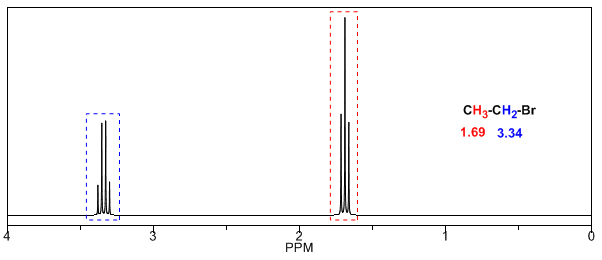
Na tabela a seguir você pode ver a influência de diferentes átomos no sinal dos hidrogênios metílicos.

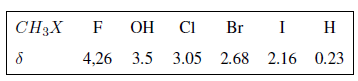
Como pode ser visto na tabela, quanto maior a eletronegatividade do grupo X, maior o deslocamento químico.

O efeito dos grupos eletronegativos é aditivo, quanto maior o número de grupos o próton fica mais desprotegido e o deslocamento é maior

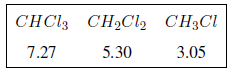
O efeito indutivo se propaga ao longo das cadeias, diminuindo seu efeito com a distância, conforme pode ser observado na tabela a seguir.

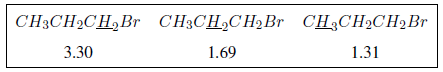
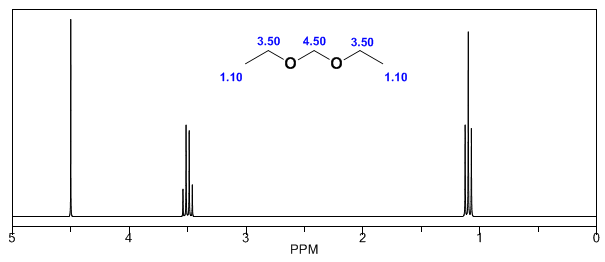
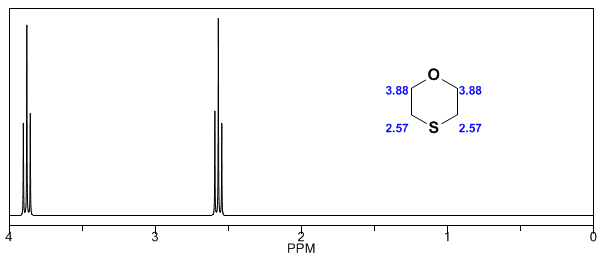
Nos espectros a seguir, podem ser observados os efeitos acima mencionados nos deslocamentos químicos.

Detalhes

Germán Fernández

RESSONÂNCIA MAGNÉTICA NUCLEAR (NMR)

Acessos: 21949

Os prótons próximos a ligações duplas e anéis aromáticos são especialmente desprotegidos devido ao campo magnético induzido pelas correntes eletrônicas desses sistemas. O campo induzido se soma ao aplicado, produzindo um deslocamento maior que o esperado.

Na imagem a seguir podemos ver a circulação eletrônica (curvas em negrito) e o campo magnético induzido (linhas tracejadas) para um alceno e uma carbonila. Observe como na região do próton o campo magnético induzido tem a mesma direção e direção do aplicado.

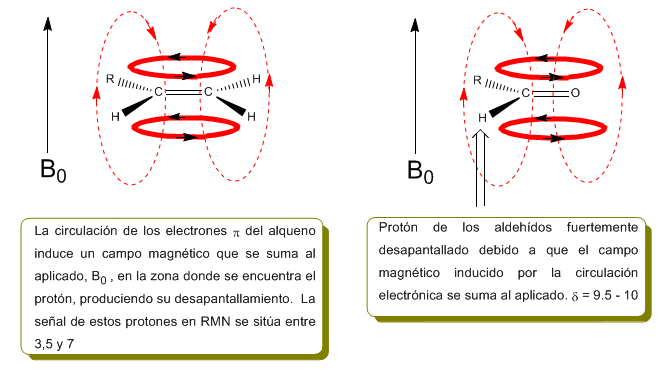
Uma situação semelhante é observada no caso do benzeno. Já nos alcinos, a circulação eletrônica induz um campo magnético oposto ao aplicado na área do próton. Os hidrogênios acetilênicos são protegidos com sinais no espectro de NMR em deslocamentos baixos.

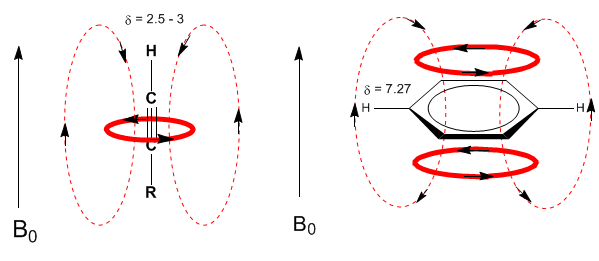
Em seguida, adiciono alguns espectros de alcenos, alcinos e aromáticos.

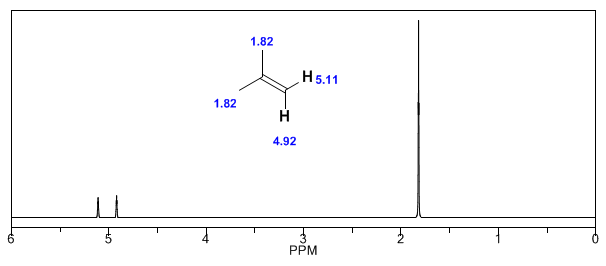
Observe como os campos induzidos aumentam consideravelmente os deslocamentos do próton olefínico, sendo as posições alílicas também afetadas.

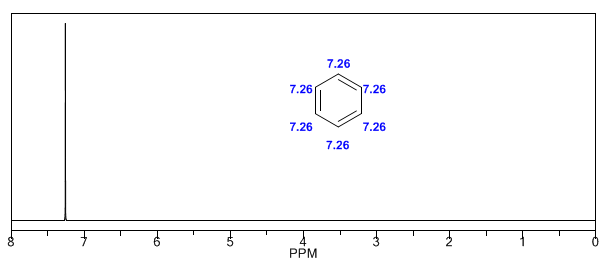
Os hidrogênios aromáticos são fortemente desprotegidos devido ao campo induzido pelas correntes do anel.

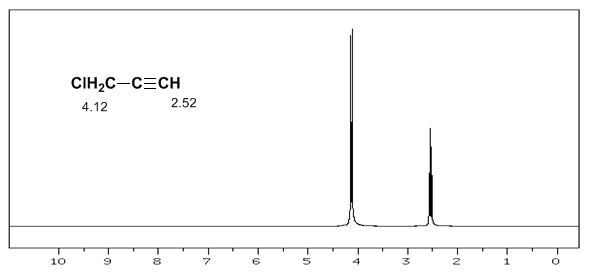
O hidrogênio acetilênico tem baixo deslocamento, pois as correntes produzem um campo magnético contrário ao aplicado.

Detalhes

Germán Fernández

RESSONÂNCIA MAGNÉTICA NUCLEAR (NMR)

Acessos: 12383

A formação de ligações de hidrogênio produz valores de deslocamento mais altos. A presença de hidrogênios ácidos pode ser detectada pela adição de água deuterada, que produz a troca de hidrogênio ácido por deutério, com o consequente desaparecimento do sinal. \begin{equation} CH_3OH + D_2O \rightleftharpoons CH_3OD + HDO \end{equation} Os deslocamentos de hidrogênio ácido mais comuns em moléculas orgânicas são:

• Ácidos carboxílicos (RCOOH) $\delta$ = 10 - 12 ppm
• Aminas ($R-NH_2$) $\delta$ = 0,5 - 5 ppm
• Amidas ($RCONH_2$) $\delta$ = 5-8 ppm
• Álcoois (ROH) $\delta$ = 0,5 - 5 ppm
• Fenóis (Ph-OH) $\delta$ = 4 - 7 ppm

Detalhes

Germán Fernández

RESSONÂNCIA MAGNÉTICA NUCLEAR (NMR)

Acessos: 26125

A informação estrutural da RMN deriva de dois fatores: os diferentes deslocamentos observados dependendo do ambiente químico que envolve o próton e o acoplamento entre os spins dos prótons próximos, que produz a divisão dos sinais.

Embora alguns sinais do espectro sejam picos únicos, é comum encontrar sinais compostos por vários picos muito próximos, que são nomeados com a seguinte notação: singleto (s), dupleto (d), tripleto (t), quadrupleto (c) , quíntuplo (q), sêxtuplo (sx) e sétuplo (sp), sinais complexos são designados como multipletos. O valor de $\delta$ destes sinais é atribuído ao seu centro, a menos que o multipleto seja irregular, caso em que o intervalo é indicado.

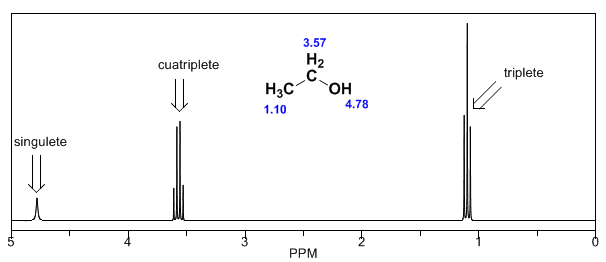
No espectro do etanol, pode-se ver que o hidrogênio da hidroxila produz um singleto, o par de hidrogênios no carbono um dá origem a um quádruplo e os três hidrogênios no carbono dois produzem um tripleto.

Explicação do acoplamento spin-spin.

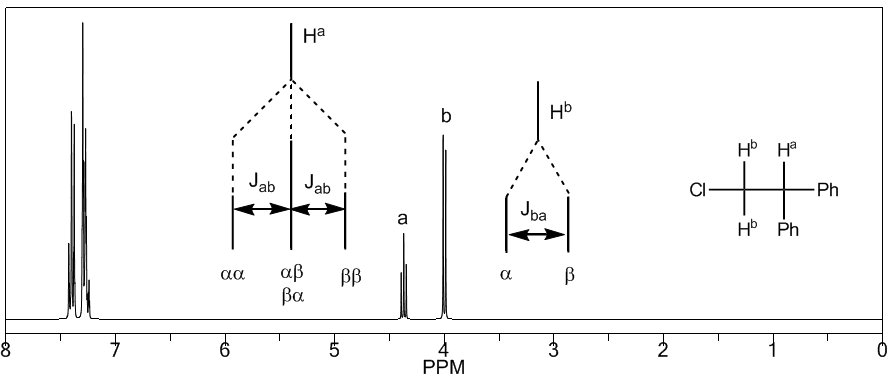
Para entender a divisão de sinais devido ao acoplamento spin-spin vamos estudar o espectro do 1,1-dicloro-2,2-difeniletano ($Cl_2CH^{a}CH^{b}Ph_2$).

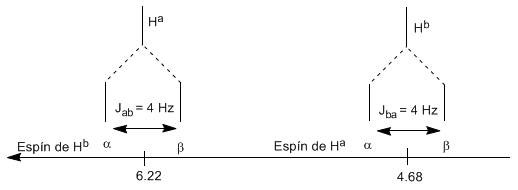
O próton $H^a$ submetido a um campo magnético $B_0$ produz um sinal a $\delta_a=6,22 ppm$. No entanto, o próton $H_b$ gera um pequeno campo magnético que afeta o próton $H_a$. Aproximadamente metade das moléculas tem o próton $H_b$ alinhado com o campo aplicado (spin alfa) e a outra metade tem ele orientado contra o campo (spin beta). Quando $H_b$ tem spin $\alpha$, $H_a$ está sujeito a um campo um pouco maior e ressoa em uma frequência mais alta ($\delta$ um pouco mais alta). Quando $H_b$ tem spin $\beta$, $H_a$ é submetido a um campo um pouco menor e ressoa em uma frequência mais baixa ($\delta$ um pouco menor), o que produz a divisão do pico inicial em dois sinais separados por um distância de 4 Hz, chamada de constante de acoplamento (J). Esse mesmo raciocínio pode ser feito para o próton $H_b$.

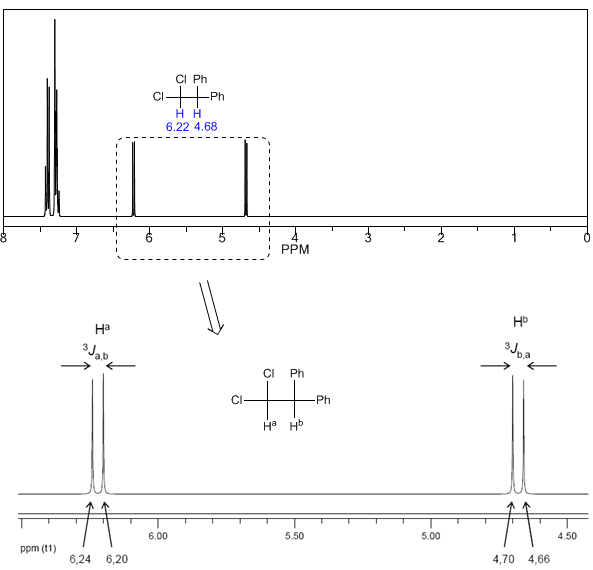
A seguir estudaremos o acoplamento de um hidrogênio $H^a$ que possui dois hidrogênios vizinhos $H^b$. Nessa situação, observa-se a divisão do sinal de hidrogênio $H^a$ em três picos (tripleto), sendo o pico central duas vezes mais intenso que os extremos. Por sua vez, os hidrogênios $H^b$ acoplam-se com $H^a$ produzindo dois picos de igual intensidade (dupleto).

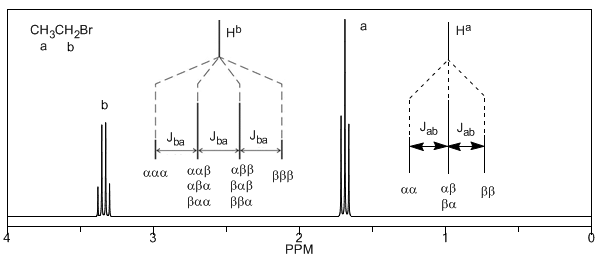
Por fim, discutiremos o acoplamento de um próton com três prótons vizinhos equivalentes. Neste caso, observa-se um sinal formado por quatro picos (quadtripleto). Os picos centrais são três vezes mais intensos que os picos extremos.

Detalhes

Germán Fernández

RESSONÂNCIA MAGNÉTICA NUCLEAR (NMR)

Acessos: 16440

Da discussão acima, pode-se deduzir que um próton produz um sinal com um número de picos uma unidade maior que o número de hidrogênios vizinhos. Na imagem a seguir podemos ver os picos produzidos por um hidrogênio $H^b$ quando acoplado a vários hidrogênios variáveis $H^a$

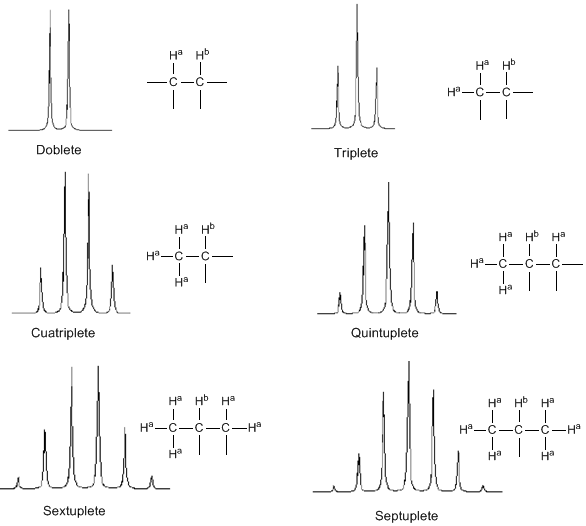
A intensidade dos picos de um sinal é dada pelo triângulo de Pascal (Tartaglia)

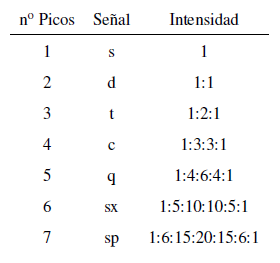
Duas considerações devem ser levadas em conta ao aplicar a regra N+1:

• Em moléculas do tipo $A-CH^{a}_2-CH^{b}_2-CH^{a}_2-A$ os prótons $H^b$ aparecem como um quíntuplo.
• Nas moléculas do tipo $A-CH_2-CH_2-A$, os quatro prótons são equivalentes e dão um singleto.

Detalhes

Germán Fernández

RESSONÂNCIA MAGNÉTICA NUCLEAR (NMR)

Acessos: 11434

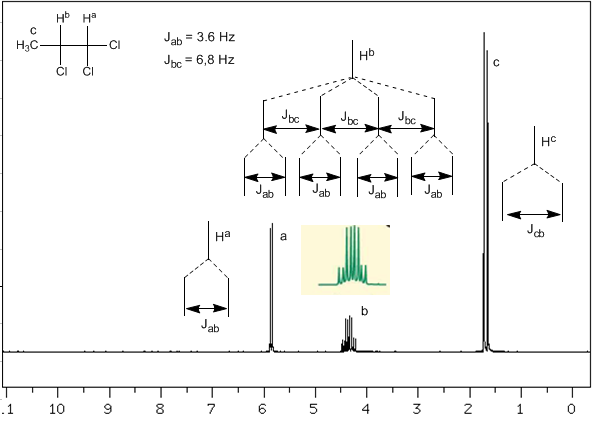
Agora vamos analisar uma situação mais complexa em que os núcleos $H^b$ apresentam diferentes constantes de acoplamento com os núcleos vizinhos $H^c$ e $H^a$. Sabendo que as constantes de acoplamento entre estes três núcleos são $J_{ab}=3.6\;Hz$ e $J_{bc}=6.8\;Hz$, para obter o sinal de $H^b$ primeiro acoplamos com $ H^c$ (maior constante de acoplamento), dando quatro picos (regra N+1), que são então acoplados com $H^a$, cada um dividido em dois picos. No total, obtém-se um sinal composto por oito picos.

Detalhes

Germán Fernández

RESSONÂNCIA MAGNÉTICA NUCLEAR (NMR)

Acessos: 13630

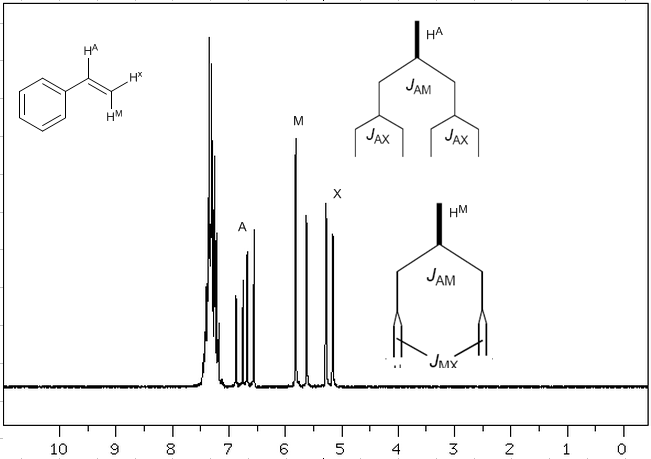
Levando em consideração que a ordem das constantes de acoplamento nos alcenos é $J_{trans}>J_{cis}>J_{geminal}$, as árvores de acoplamento para os hidrogênios $H^a$ e $H^M$ são as indicadas na o espectro. Você seria capaz de desenhar a árvore para $H^x$?