Details

Germán Fernández

Nuclear Magnetic Resonance (NMR)

Hits: 13647

Atomic nuclei rotate on themselves (spin) and present an angular momentum that is given by the expression \begin{equation}\label{ec1} L=\sqrt{I(I+1)}\hbar \end{equation} Angular momentum depends on the quantum number I (angular momentum quantum number or nuclear spin), which can take different values depending on the type of nucleus, I=0, 1/2, 1, 3/2, 2, 5/2, 3,.....

The calculation of the spin quantum number for a nucleus is done by adding the spins of unpaired protons and neutrons. For example, hydrogen has I=1/2, as it is made up of only one proton.

The allowed quantum spin states are given by $m_I$, which takes the following values \begin{equation} m_I=-I, -I+1, ...., I-1, I \end{equation} The number of values that $m_I$ takes for a given value of I is $2I+1$. Thus, for a nucleus with I=1/2 there are two possible quantum spin states given by $m_I=-1/2, 1/2$. A nucleus with I=1 has three allowed spin quat states $m_I=-1, 0, +1$. In the absence of a magnetic field, the spin quantum states are degenerate.

Details

Germán Fernández

Nuclear Magnetic Resonance (NMR)

Hits: 13779

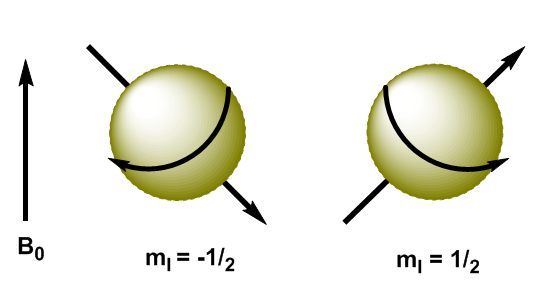
Atomic nuclei are charged particles and their angular momentum produces magnetic momentum, represented by $\mu$ \begin{equation}\label{ec3} \mu=\gamma L = \gamma \sqrt{I(I+1)} \hbar \end{equation} where $\gamma$ is the gyromanetic constant, characteristic of each nucleus. When we apply a magnetic field, $B_0$, to nuclei with I=1/2, the magnetic moments are oriented in such a way that the nuclei with $m_I=1/2$ have their magnetic moment aligned with the field and the nuclei with $ m_I=-1/2$ have their magnetic moment opposite to the applied field.

Details

Germán Fernández

Nuclear Magnetic Resonance (NMR)

Hits: 11212

In quantum mechanics the magnetic angular momentum in the z direction is given by $L_z=m_I\hbar$. The kernel with $m_I=1/2$ has $L_z=1/2\hbar$, while the kernel with $m_I=-1/2$ has $L_z=-1/2\hbar$. The magnetic moment in this direction is $\mu_z=\gamma L_z$.

These equations allow us to determine the energy of both levels. \begin{equation}\label{ec4} E=-\mu_zB_0=-\gamma m_I\hbar B_0 \end{equation} Now we can calculate the energy difference between the two levels \begin{equation}\label{ec6} \Delta E=-\gamma (-1/2)\hbar B_0 + \gamma 1/2\hbar B_0=\gamma\hbar B_0 \end{equation}

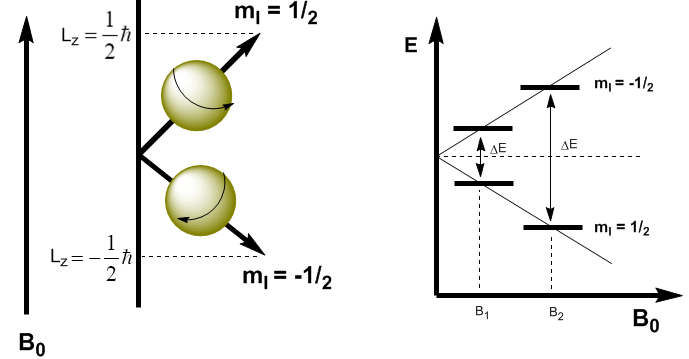
As can be seen in the equation (\ref{ec6}) the energy difference depends on the applied magnetic field. If the magnetic field is low, $\Delta E$ is small and the population difference between the two levels is also small, which causes a sensitivity problem. At high magnetic fields we have a significant separation between levels, which gives rise to a high population difference, obtaining greater sensitivity.

Details

Germán Fernández

Nuclear Magnetic Resonance (NMR)

Hits: 13649

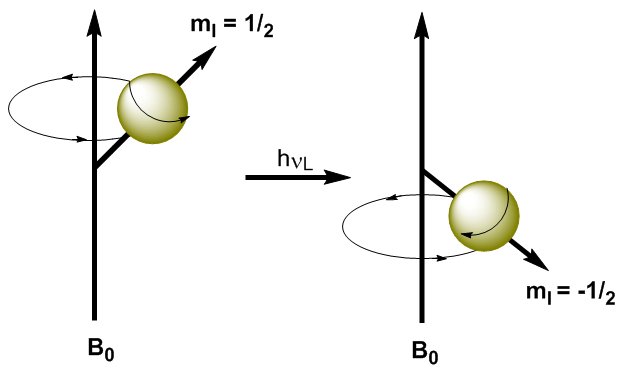
By applying electromagnetic radiation of suitable frequency (radio waves) it is possible to promote the nuclei from the lower energy level ($m_I=1/2$) to the higher energy level ($m_I=-1/2$). When electromagnetic radiation and the precession of the nucleus enter into resonance, absorption occurs. We can calculate the resonant frequency (Larmor frequency) using Planck's equation. \begin{equation}\label{ec7} \Delta E = h\nu_L \end{equation} Substituting the difference in energy for the equation (\ref{ec7}) \begin{equation}\label{ec8} \gamma\ hbar B_0=h\nu_L \end{equation} Solving for the Larmor Frequency \begin{equation}\label{ec10} \nu_L=\frac{\gamma}{2\pi}B_0 \end{equation} As can be seen in the equation (\ref{ec10}) the frequency at which the transition occurs depends on the applied magnetic field. The increase in the magnetic field produces an increase in the energy difference between the spin levels, so a higher frequency radiation is required to produce the transition.

Details

Germán Fernández

Nuclear Magnetic Resonance (NMR)

Hits: 16623

In Magnetic resonance, nuclei with spin angular momentum other than zero are used, such as $^1H$ and $^{13}C$. However, the resonance frequencies are not the same for all hydrogen or carbon nuclei, they depend on the chemical environment that surrounds each nucleus. This is due to the fact that the electrons surrounding each nucleus generate a magnetic field that opposes the applied one, it is said that the nuclei are shielded, where $\sigma$ is the shielding constant. \begin{equation}\label{ec11} B_{eff}=B_0-\sigma B_0=(1-\sigma)B_0 \end{equation} $B_{ef}$ is the net magnetic field acting on the proton; $B_0$ is the applied magnetic field; $\sigma$ is the screening constant, independent of the applied field. Under this new situation, with the nuclei shielded by the surrounding electron density, the resonance frequency becomes \begin{equation}\label{ec12} \nu=\frac{\gamma}{2\pi}(1 -\sigma)B_0 \end{equation} Nuclei with different chemical environments have a different screening constant, generating different signals in the NMR spectrum.

Details

Germán Fernández

Nuclear Magnetic Resonance (NMR)

Hits: 21946

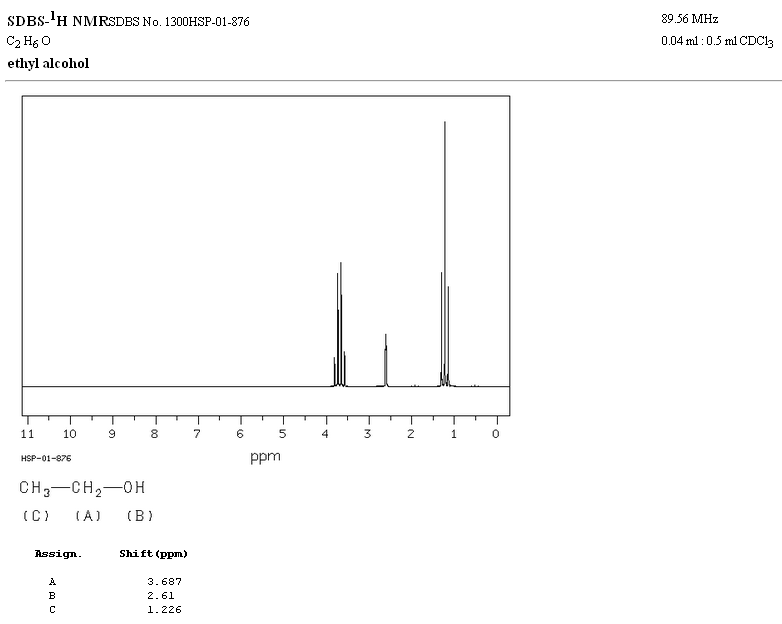
In the NMR spectrum of ethanol, three different signals are observed, due to the existence of 3 types of hydrogens with different chemical environments. Hydrogens A are more unshielded than C due to the presence of oxygen (electronegative atom that removes electron density). The chemical environment of hydrogen B, directly attached to oxygen, is also different, resonating at a different frequency from the previous ones.

Details

Germán Fernández

Nuclear Magnetic Resonance (NMR)

Hits: 23778

Signals in the NMR spectrum are measured on a scale independent of the applied magnetic field, called the chemical shift and represented by the letter $\delta$. Regardless of the magnetic field at which the spectrophotometer works, the signals of a chemical compound are always obtained at the same values of $\delta$. \begin{equation} \delta=\frac{\nu_{sample}-\nu_{reference}}{\nu_{reference}}\cdot 10^6 \end{equation} By definition is taken as zero of the scale of chemical shift the signal from tetramethylsilane ($Si(CH_3)_4$). Let's calculate the chemical shift for $CH_3Br$ knowing that in a 90 MHz device the absorption frequency occurs at 90 000 237 Hz. \begin{equation} \delta =\frac{90 000 237 - 90 000 000}{ 90 000 000}\cdot 10^{6}=2.63 \end{equation} In a spectrophotometer working at 300 MHz the absorption occurs at 300 000 790 Hz, repeating the previous calculation the same chemical shift is obtained.\ \ The more unshielded hydrogens come out at larger displacements: $CH_3Br\rightarrow \delta =2.63$; $CH_2Br_2\rightarrow \delta =$4.90; $CHBr_3\rightarrow \delta = $6.82

Details

Germán Fernández

Nuclear Magnetic Resonance (NMR)

Hits: 28431

The following table shows the ranges in which the NMR signals appear for different types of hydrogens.

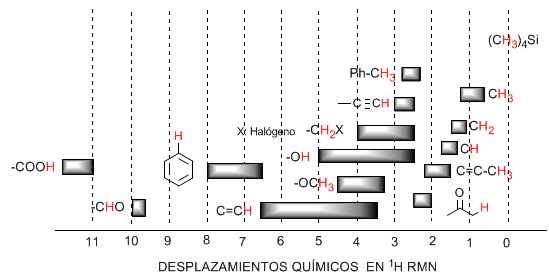
♦ Hydrogens located on aliphatic chains present values of $\delta$ close to 1. They increase slightly when going from primary to secondary or tertiary carbons.

♦ Allylic hydrogens are located between 1.5 and 2.1.

♦ Alpha hydrogens with respect to carbonyls and acid derivatives are between 2 and 2.5.

♦ The benzylic hydrogens between 2.3 and 2.7.

♦ The hydrogen of terminal alkynes between 2.5 and 3.

♦ Hydrogens attached to carbons with halogens between 2.5 and 4 depending on the electronegativity of the halogen

♦ The hydrogens of the hydroxyl group between 2.5 and 5. Very wide range due to the formation of hydrogen bonds.

♦ Hydrogens with ether-type oxygen bonded carbons between 3.3 and 4.5.

♦ Olefinic hydrogens between 3.5 and 6.5.

♦ Hydrogens bound to aromatic systems between 6.5 and 8.

♦ Hydrogen from aldehydes 9.5-10

♦ Hydrogen from carboxylic acid group above 11.

Details

Germán Fernández

Nuclear Magnetic Resonance (NMR)

Hits: 15018

Electronegative substituents remove electron density, unshielding the hydrogens, and shift the signal toward high \delta$ values.

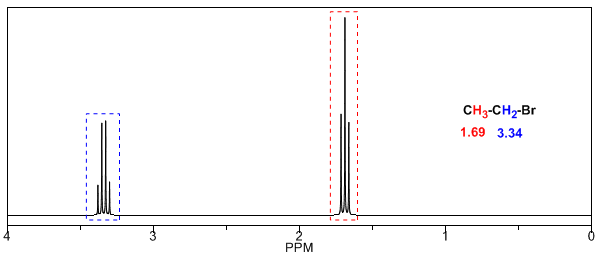
In the following table you can see the influence of different atoms on the signal of the methyl hydrogens.

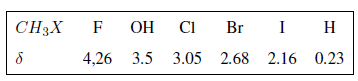
As can be seen in the table, the greater the electronegativity of group X, the greater the chemical shift.

The effect of the electronegative groups is additive, the greater the number of groups the proton is more unshielded and the displacement is greater

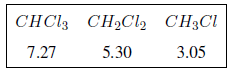
The inductive effect propagates along the chains, decreasing its effect with distance, as can be seen in the following table.

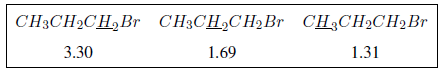
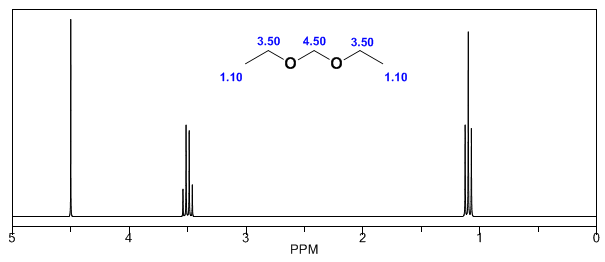
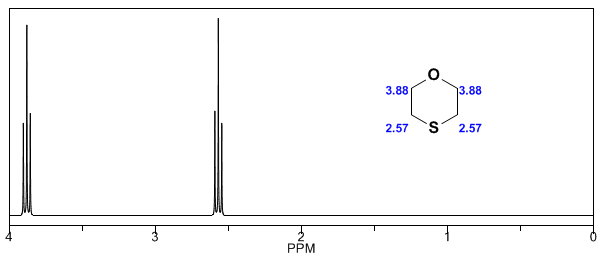
In the following spectra, the aforementioned effects on chemical shifts can be observed.

Details

Germán Fernández

Nuclear Magnetic Resonance (NMR)

Hits: 22124

The protons close to double bonds and aromatic rings are especially unshielded due to the magnetic field induced by the electronic currents of these systems. The induced field is added to the applied one, producing a displacement greater than expected.

In the following image we can see the electronic circulation (curves in bold) and the induced magnetic field (dashed lines) for an alkene and a carbonyl. Observe how in the region of the proton the induced magnetic field has the same direction and direction as the applied one.

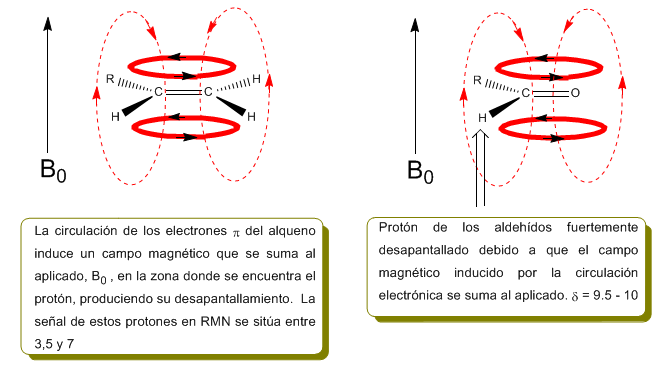
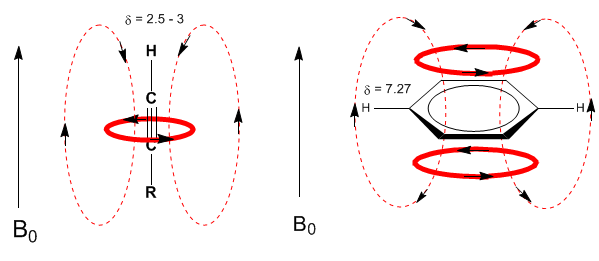
A similar situation is observed in the case of benzene. However, in alkynes, electronic circulation induces a magnetic field that opposes the one applied in the proton area. The acetylenic hydrogens are shielded with signals in the NMR spectrum at low offsets.

Next, I add some spectra of alkenes, alkynes, and aromatics.

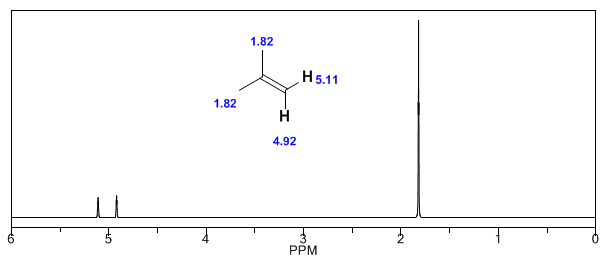
Observe how the induced fields considerably increase the displacements of the olefinic proton, the allylic positions being also affected.

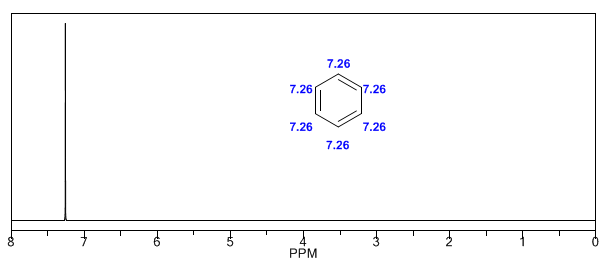
The aromatic hydrogens are strongly unshielded due to the field induced by the ring currents.

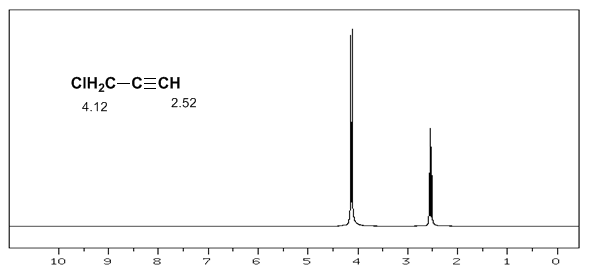
The acetylenic hydrogen has a low displacement, because the currents produce a magnetic field that opposes the applied one.

Details

Germán Fernández

Nuclear Magnetic Resonance (NMR)

Hits: 12364

The formation of hydrogen bonds produces higher displacement values. The presence of acidic hydrogens can be detected by adding deuterated water, which produces the exchange of acidic hydrogen for deuterium, with the consequent disappearance of the signal. \begin{equation} CH_3OH + D_2O \rightleftharpoons CH_3OD + HDO \end{equation} The most common acid hydrogen shifts in organic molecules are:

• Carboxylic acids (RCOOH) $\delta$ = 10 - 12 ppm
• Amines ($R-NH_2$) $\delta$ = 0.5 - 5 ppm
• Amides ($RCONH_2$) $\delta$ = 5-8 ppm
• Alcohols (ROH) $\delta$ = 0.5 - 5 ppm
• Phenols (Ph-OH) $\delta$ = 4 - 7 ppm

Details

Germán Fernández

Nuclear Magnetic Resonance (NMR)

Hits: 26154

The structural information of NMR derives from two factors: the different displacements observed depending on the chemical environment that surrounds the proton and the coupling between the spins of nearby protons, which produces the splitting of the signals.

Although some signals in the spectrum are single peaks, it is common to find signals composed of several very close peaks, which are named with the following notation: singlet (s), doublet (d), triplet (t), quadruplet (c), quintuplet ( q), sextuplet (sx) and septuplet (sp), complex signals are designated as multiplets. The value of $\delta$ of these signals is assigned to their center, unless the multiplet is irregular, in which case the interval is indicated.

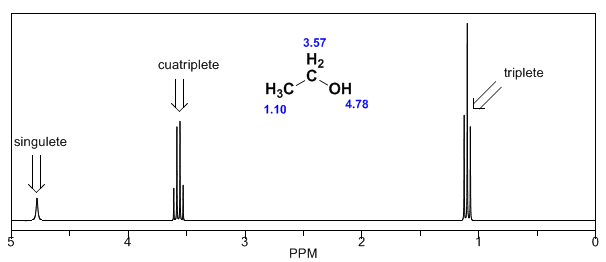
In the spectrum of ethanol it can be seen that the hydroxyl hydrogen produces a singlet, the pair of hydrogens on carbon one give rise to a quadruplet, and the three hydrogens on carbon two produce a triplet.

Explanation of spin-spin coupling.

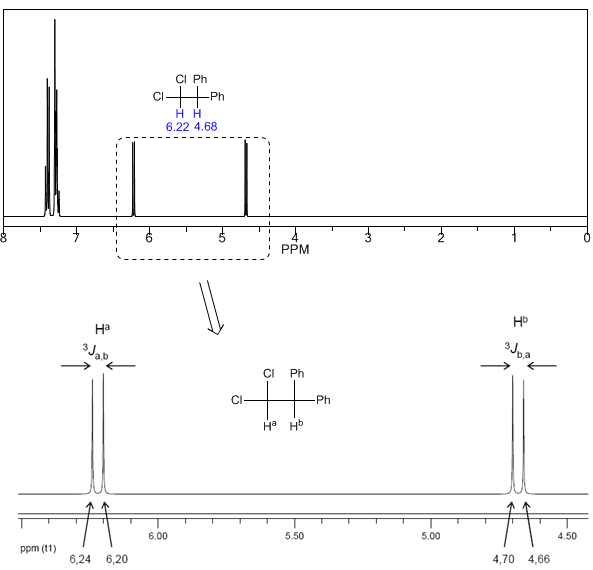
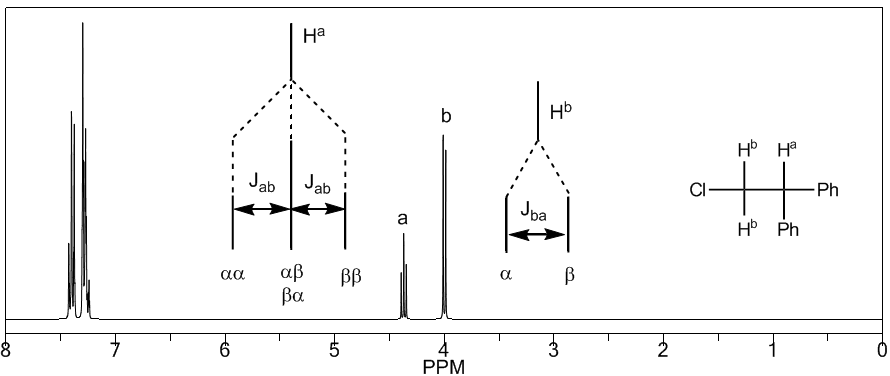
To understand the splitting of signals due to spin-spin coupling we are going to study the spectrum of 1,1-dichloro-2,2-diphenylethane ($Cl_2CH^{a}CH^{b}Ph_2$).

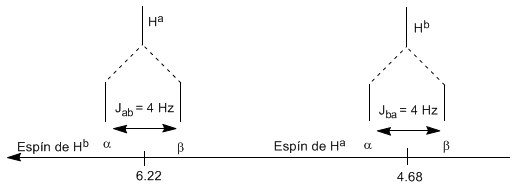
The proton $H^a$ subjected to a magnetic field $B_0$ produces a signal at $\delta_a=6.22 ppm$. However, the proton $H_b$ generates a small magnetic field that affects the proton $H_a$. Approximately half of the molecules have the $H_b$ proton aligned with the applied field (alpha spin) and the other half have it oriented against the field (beta spin). When $H_b$ has spin $\alpha$, $H_a$ is subjected to a slightly larger field and resonates at a higher frequency ($\delta$ slightly higher). When $H_b$ has spin $\beta$, $H_a$ is subjected to a slightly smaller field and resonates at a lower frequency ($\delta$ slightly lower), which produces the splitting of the initial peak into two signals separated by a distance of 4 Hz, called the coupling constant (J). This same reasoning can be done for the proton $H_b$.

Next, we will study the coupling of a hydrogen $H^a$ that has two neighboring hydrogens $H^b$. In this situation, the splitting of the hydrogen signal $H^a$ into three peaks (triplet) is observed, the central peak being twice as intense as the extreme ones. For their part, the hydrogens $H^b$ couple with $H^a$ producing two peaks of equal intensity (doublet).

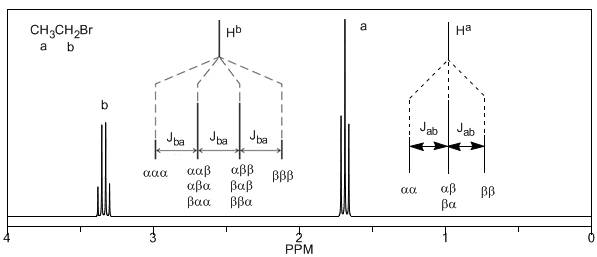
Lastly, we will discuss the coupling of a proton with three equivalent neighboring protons. In this case, a signal made up of four peaks (quadtriplet) is observed. The central peaks are three times as intense as the extreme peaks.

Details

Germán Fernández

Nuclear Magnetic Resonance (NMR)

Hits: 16649

From the above discussion it can be deduced that a proton produces a signal with a number of peaks one unit greater than the number of neighboring hydrogens. In the following image we can see the peaks produced by a hydrogen $H^b$ when coupled with a number of variable hydrogens $H^a$

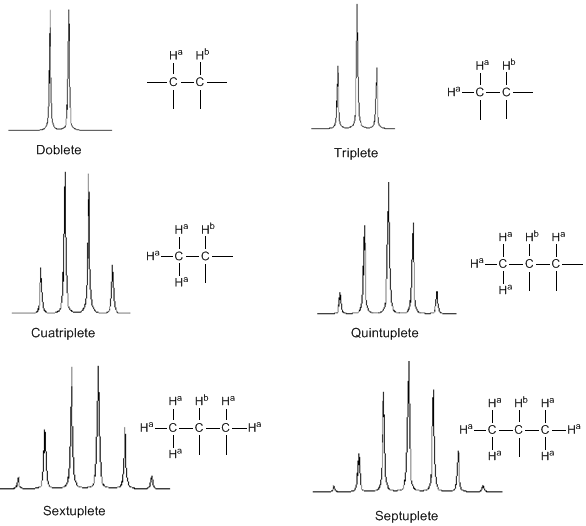
The intensity of the peaks of a signal are given by Pascal's triangle (Tartaglia)

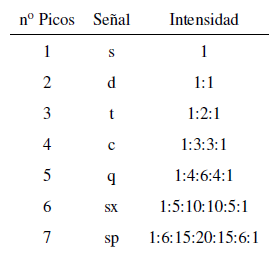
Two considerations must be taken into account when applying the N+1 rule:

• In molecules of the type $A-CH2^{a}-CH2}^{b}-CH2}^{a}-A$ the $H^b$ protons appear as a quintuplet.
• In molecules of the type $A-CH_2-CH_2-A$, the four protons are equivalent and give a singlet.

Details

Germán Fernández

Nuclear Magnetic Resonance (NMR)

Hits: 11488

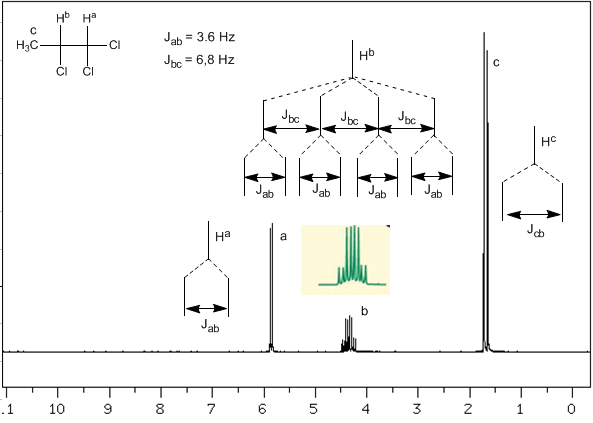
Now we will analyze a more complex situation in which the nuclei $H^b$ present different coupling constants with the neighboring nuclei $H^c$ and $H^a$. Knowing that the coupling constants between these three nuclei are $J_{ab}=3.6\;Hz$ and $J_{bc}=6.8\;Hz$, to obtain the signal of $H^b$ we first couple it with $ H^c$ (greatest coupling constant), giving four peaks (N+1 rule), which are then coupled with $H^a$, each splitting into two peaks. In total, a signal made up of eight peaks is obtained.

Details

Germán Fernández

Nuclear Magnetic Resonance (NMR)

Hits: 13685

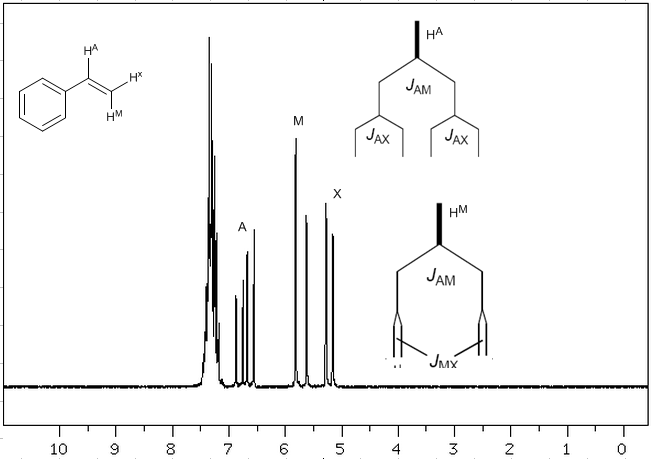
Taking into account that the order of coupling constants in alkenes is $J_{trans}>J_{cis}>J_{geminal}$, the coupling trees for the hydrogens $H^a$ and $H^M$ are the indicated on the spectrum. Would you be able to draw the tree for $H^x$?