Kernspinresonanz

Kernspinresonanz (NMR)-Techniken sind ein unverzichtbares Instrument für die Chemie sowie für andere Wissenschaftszweige. Mit der NMR-Spektroskopie kann man Moleküle identifizieren (ein Spektrum darstellen), ihre Struktur bestimmen oder dynamische Prozesse untersuchen. Zum Beispiel war es der Schlüssel zur Bestimmung der Struktur von Proteinen in Lösung, und andererseits sind bildgebende NMR-Techniken ein unverzichtbares Werkzeug in der medizinischen Diagnose, wie in (Abbildung b) dargestellt.

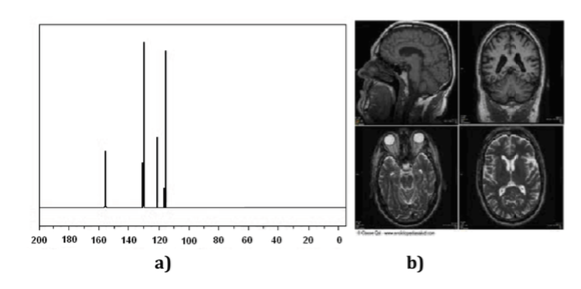
NMR basiert auf drei Elementen:

a) Der magnetische Charakter der Kerne der untersuchten Moleküle:

Viele Atomkerne haben aufgrund des Kernspins magnetische Eigenschaften. In gewisser Weise kann man davon ausgehen, dass sich die Kerne wie kleine Magnete verhalten.

b) Die Anwendung eines starken Magnetfelds:

Wenn die untersuchten Moleküle in ein Magnetfeld eingetaucht werden, entfalten sich die nuklearen Ebenen in verschiedene Energieniveaus. Jedes der auftretenden Energieniveaus entspricht unterschiedlichen Ausrichtungen der Spins der Kerne (kleine Magnete) in Bezug auf das Magnetfeld.

c) Beleuchtung der Probe mit elektromagnetischer Strahlung:

Wie bei anderen spektroskopischen Techniken bewirkt die Beleuchtung der Probe mit der angemessenen Strahlungsfrequenz, dass die Kerne von einer Ebene zur anderen übergehen. Die zur Erzeugung dieses Pegelsprungs erforderliche Strahlungsfrequenz hängt von der Art des Kerns, seiner chemischen Umgebung, der Art der in seiner Nähe vorhandenen Kerne und dem angelegten externen Feld ab. In diesem Thema werden die physikalischen Grundlagen dieser Technik untersucht und die experimentellen Techniken erklärt, die es ermöglichen, die Spektren zu erhalten, wobei auch die Ursachen analysiert werden, die die Spektren der verschiedenen Moleküle unterschiedlich machen.

Grundlagen der NMR:

Kernspin und Drehimpuls des Kernspins

Atomkerne bestehen aus Protonen und Neutronen. Beide Nukleonen haben Bahndrehimpuls und Spindrehimpuls (sowohl Protonen als auch Neutronen haben Spin 1/2). Die Resultierende der Vektorsumme aller Momente (Orbital und Spin) aller Protonen und Neutronen des Kerns ergibt als Ergebnis den Kernspin-Drehimpuls und wird durch I symbolisiert und seine Einheiten sind J s. Gemäß der Quantenmechanik ist die Größe des Kernspindrehimpulses, |I|, quantisiert, mit einem Wert I(I+1)h, wobei I die Kernspinquantenzahl oder der Kernspin ist und ħ h/2p ist (was im internationalen System ist es 1,05457·10-34J·s wert). Der Wert von I ist eine feste Eigenschaft jedes Atomkerntyps und kann einen ganzzahligen oder halbzahligen Wert annehmen (0,1, 2, 3,… ½ , 3/2 , 5/2…).

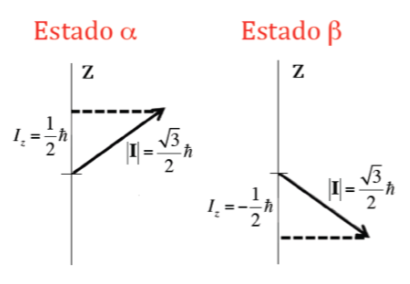
Neben dem Modul ist es auch wichtig, die Komponente des Drehimpulses um die z-Achse, Iz, zu kennen. Dies kann auch quantisierte Werte annehmen, die durch den Ausdruck m I h gegeben sind, wobei m I die Quantenzahl ist, die der z-Komponente des Kernspin-Drehimpulses zugeordnet ist, und die die folgenden Werte annehmen kann: –I, (-I+1) , ... , (I-1), I. Somit gibt es für einen gegebenen Kern mit einem Wert von I (2I+1) Orientierungen des Drehimpulses des Kernspins. Betrachten Sie zum Beispiel den Atomkern des häufigsten Isotops des Wasserstoffatoms, 1H, das von einem Proton gebildet wird, und es ist bekannt, dass sein Kernspin I 1/2 beträgt, und daher kann m I zwei Werte annehmen ​+1 /2 und ‐1/2 (im NMR wird das 1H-Isotop oft als Proton bezeichnet). Das Proton hat also zwei mögliche Kernzustände, einen namens a mit m I =+1/2 und den anderen b mit m I =‐1/2. Die folgende Abbildung zeigt die zwei möglichen Orientierungen des Kernspin-Drehimpulses, die den Zuständen a und b entsprechen, die energetisch äquivalent sind.

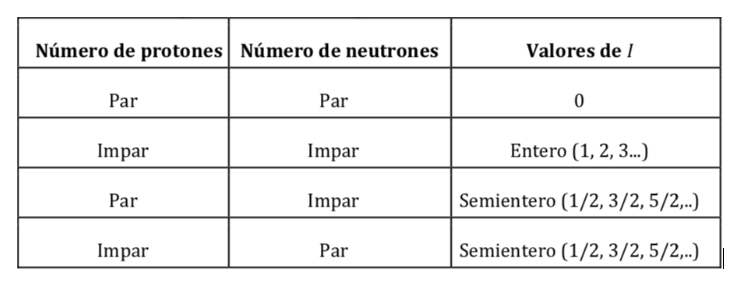
Werte von I nach der Anzahl der Protonen und Neutronen im Kern:

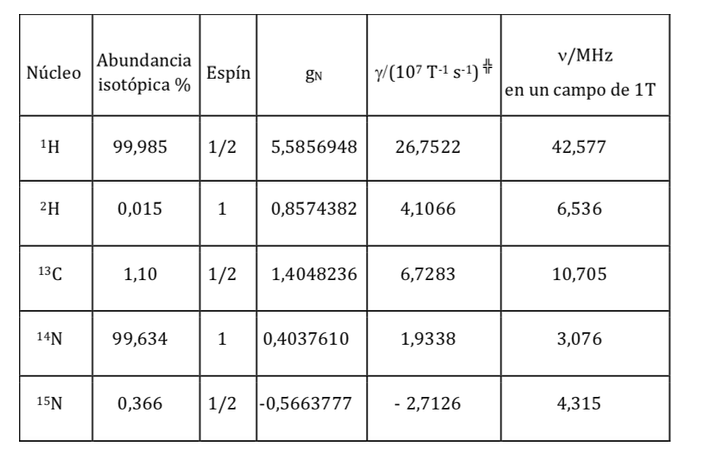
Magnetische Eigenschaften verschiedener Kerne:

Kernmagnetisches Dipolmoment (Kernmagneton, gyromagnetisches Verhältnis):

So wie das Elektron ein magnetisches Dipolmoment hat, haben einige, aber nicht alle Atomkerne ein magnetisches Dipolmoment. Wie angedeutet, verhalten sich die Kerne wie kleine Magnete, wobei der Ursprung dieses magnetischen Charakters im Drehimpuls des Kernspins liegt. Aus dem Kernspin-Drehimpuls I ergibt sich ein kernmagnetisches Dipolmoment mI, das gegeben ist durch:

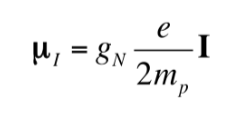
wobei gN der nukleare g-Faktor ist. Beachten Sie, dass dieser Ausdruck per Definition die Masse und Ladung des Protons (mp ye) anstelle der Masse und Ladung des betreffenden Kerns verwendet. Die Unterschiede von einem Kern zum anderen sind im Kern-gN-Faktor enthalten. Der Wert von gN kann nicht theoretisch erhalten werden, also wird er experimentell bestimmt. Die Einheiten von mI sind JT-1

Die Beziehung zwischen mI und I kann auch wie folgt ausgedrückt werden:

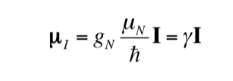
mit

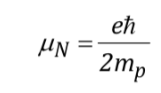
wobei eine Konstante mit einem Wert von 5.050 10-27J T-1 Kernmagneton genannt wird und g die gyromagnetische Beziehung (T-1s-1) ist In den vorherigen Tabellen wurden für einige Isotope bereits Werte dieser Größen angegeben. Obwohl in den meisten Fällen mI und I den gleichen Sinn haben, ist es manchmal auch umgekehrt, wie sich zum Beispiel aus den negativen Werten der Faktoren gN und g für das 15N-Isotop ableiten lässt.

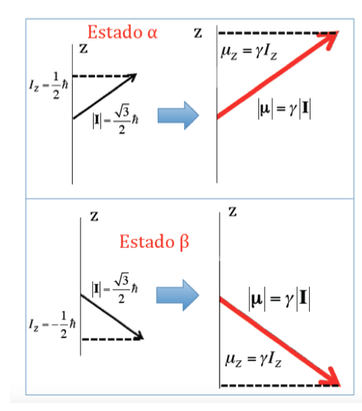
Im Fall des Protons, bei dem zwei mögliche Orientierungen des Drehimpulses gesehen wurden, gibt es zwei mögliche Orientierungen des magnetischen Dipolmoments, wie in der folgenden Abbildung dargestellt, wobei beide Orientierungen energetisch äquivalent sind, da die Wahl einer z-Richtung ist willkürlich.

Wechselwirkungsenergie des Magnetfeldes mit dem kernmagnetischen Moment:

Wenn ein Molekül in ein Magnetfeld mit Flussdichte oder Magnetfeld B eingeführt wird, wird das magnetische Dipolmoment jedes seiner Kerne mit ihm interagieren, wie in der folgenden Abbildung dargestellt, wobei die Energie der Wechselwirkung ausgedrückt wird durch:

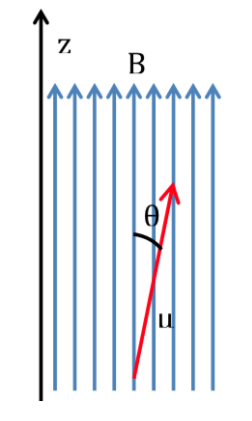
Gemäß der klassischen Physik sind alle Orientierungen eines magnetischen Dipols innerhalb eines Magnetfelds erlaubt und daher kann q jeden Wert zwischen 0 und 180o annehmen. Je nach Ausrichtung des Dipols ist die Energie höher oder niedriger:

Die günstigste Wechselwirkung tritt auf, wenn beide Größen die gleiche Richtung haben: q=0 und damit cos q=1 und :

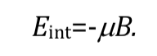
Allerdings sind laut Quantenmechanik nicht alle Orientierungen des kernmagnetischen Dipols erlaubt, die Orientierungen sind quantisiert und nur bestimmte Werte von q sind möglich. Es sind so viele Orientierungen erlaubt wie Iz- oder mI-Werte (-I, -I+1,..., I-1, I), also 2I+1-Orientierungen. Offensichtlich variiert die Anzahl der Orientierungen des Dipolmoments mit der Art des Atomkerns. Um die Orientierungen zu definieren, wird die Richtung und Richtung des Feldes B als Referenz für die Z-Achse genommen.

Somit ist die Wechselwirkungsenergie des äußeren Magnetfeldes B und des Kerndipols gegeben durch: j

Langmor-Frequenz

Wenn ein externes Magnetfeld der Intensität B auf den Kern einwirkt, erfährt der nukleare magnetische Dipol einige Kräfte, wie in der folgenden Formel gezeigt:

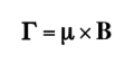
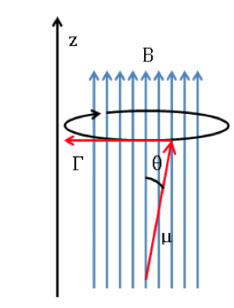
was dazu neigt, den Dipol mit dem Magnetfeld auszurichten. Da der magnetische Dipol nicht auf das Magnetfeld ausgerichtet werden kann, ist das System nicht in der Lage, diese Energie abzuleiten und präzediert, die so genannte Larmor-Präzession

über die Richtung des angelegten Feldes. Die Frequenz dieser Präzession wird Larmor-Frequenz genannt, mit einem Wert:

Langmor-Schema:

NMR-Spektroskopie

Der Schlüssel zu jeder spektroskopischen Technik basiert auf der Möglichkeit, dass sich das zu untersuchende Molekül auf mehr als einem Energieniveau befinden kann, so dass es durch Beeinflussung durch elektromagnetische Strahlung (rem) der entsprechenden Frequenz in unser System gelangen kann (Molekül) von einem Energieniveau zum anderen. Wie im vorherigen Abschnitt gesehen, kann der Kern eines Protons, der in ein Magnetfeld eingetaucht ist, zwei verschiedene Ebenen einnehmen, die dem Kernspin zugeordnet sind, wodurch ein Rem-Strahl der entsprechenden Frequenz auf einen 1H-Kern fällt, der die untere Ebene einnimmt. es kann an die obere Ebene weitergegeben werden. Diese Art von Übergängen führt zur kernmagnetischen Resonanzspektroskopie (NMR). Von nun an konzentrieren wir uns auf den Fall des 1H-Protons, da es die am häufigsten verwendete Spektroskopie ist, obwohl alles Angegebene auf andere Kerne anwendbar ist. Tatsächlich werden immer mehr verschiedene Kerne verwendet.

Resonanzfrequenz:

Die Frequenz, die den Übergang verursacht, wird durch Anwendung der Resonanzbedingung erhalten:

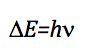
Da die Energiedifferenz zwischen zwei aufeinanderfolgenden Niveaus ist:

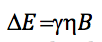
beide Ausdrücke gleichsetzen und n isolieren:

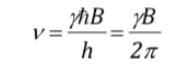
was, wie man sehen kann, mit der Larmor-Präzessionsfrequenz zusammenfällt.

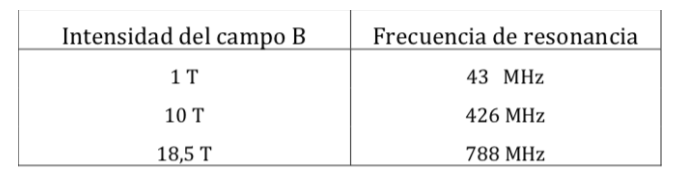
Protonen-NMR-Resonanzfrequenzen für verschiedene Feldstärken:

Auswahlregeln:

Die in anderen Spektroskopien untersuchten Auswahlregeln entsprechen der Wechselwirkung des elektrischen Dipols mit dem elektrischen Feld der Strahlung. Andererseits tritt bei der NMR die Wechselwirkung zwischen dem magnetischen Dipol des Kerns und dem variablen Magnetfeld der Strahlung auf. Um die Auswahlregeln zu bestimmen, muss man sich den allgemeinen Ausdruck merken, der die Übergangswahrscheinlichkeit zwischen zwei Zuständen bestimmt:

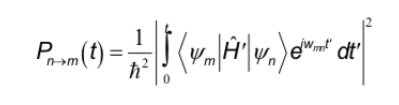
Der Hamiltonoperator ist in diesem Fall das Produkt des Operators des oszillierenden Magnetfelds der Strahlung mit dem Operator des Dipolmoments des Kerns.

Es kann gezeigt werden, dass für einen Übergang zwischen zwei Ebenen die entsprechende Auswahlregel lautet:

m ich = ± 1

Signalstärke (Bevölkerungsdichte):

Die Signalintensität steht in direktem Zusammenhang mit der Population der am Übergang beteiligten Ebenen. Gemäß dem Verteilungsgesetz von Boltzman ist für ein Zwei-Ebenen-System wie das Proton das Verhältnis der Besetzung der oberen Ebene, Nb, und der Besetzung der unteren Ebene, Na, gegeben durch:

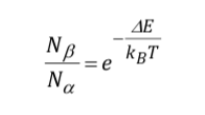
Beschreibung der NMR-Ausrüstung:

Welches experimentelle Verfahren wird verwendet, um das Spektrum zu erhalten? Im Allgemeinen wird in der Spektroskopie die Frequenz der einfallenden Strahlung variiert, bis eine Absorption beobachtet wird. Bei der NMR-Spektroskopie besteht jedoch auch die Möglichkeit, die Strahlungsfrequenz festzuhalten und den Abstand zwischen den Niveaus zu variieren, indem die Größe des angelegten Felds B variiert wird, bis eine Absorption beobachtet wird. In der folgenden Abbildung ist ein Schema einer NMR-Ausrüstung dargestellt. Die Probe wird in ein Röhrchen gegeben, das manchmal schnell gedreht wird, um eine Homogenisierung des Signals zu erreichen, obwohl die Verwendung der Rotation derzeit diskutiert wird, da sie Fehler einführen kann. Das Rohr wiederum befindet sich zwischen zwei Magnetpolen, die das Magnetfeld erzeugen. Es gibt einen Sender und einen Empfänger von Funkfrequenzen. Das Emittersignal kann so gesteuert werden, dass es einen Frequenz-Sweep durchführt. Mit Sweep-Spulen kann ein Sweep des Feldes gesteuert werden. Aktuelle NMR-Geräte verwenden fast keine mehr:

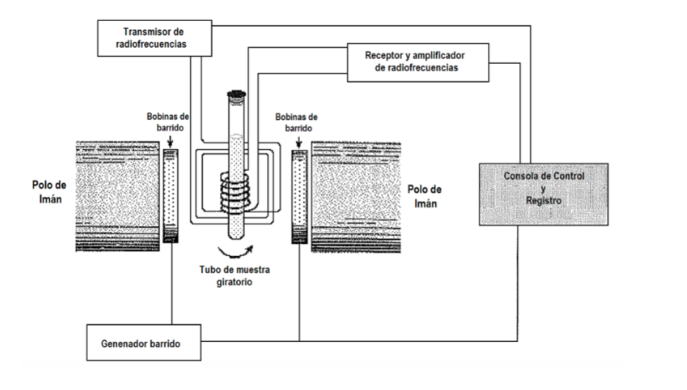
früheren Verfahren, basieren jedoch auf der Verwendung von Fourier-Transformationstechniken. B wird stationär gehalten und die Probe wird mit einem zeitlich begrenzten Hochfrequenzimpuls hoher Leistung mit der Frequenz nrad beleuchtet, einem festen Wert im NMR-Frequenzbereich des untersuchten Kerntyps. Der Impuls dauert mehrere Mikrosekunden, sodass mathematisch durch eine Technik namens Fourier-Analyse gezeigt werden kann, dass der Hochfrequenzimpuls einem Bereich von Frequenzen ∆n um nrad entspricht und alle möglichen NMR-Resonanzen anregt. Das im Detektor beobachtete Signal enthält alle Resonanzfrequenzen und wird von einem Computer unter Verwendung von Fourier-Transformationstechniken analysiert. Dieses Verfahren ermöglicht eine sehr hohe Auflösung und das Arbeiten mit Kernen, die bei den vorherigen Verfahren sehr schwache Signale hatten.

Nukleare Abschirmung:

In der Magnetresonanz werden Kerne mit einem anderen Spindrehimpuls als Null verwendet, wie z. B. 1H und 13C. Die Resonanzfrequenzen sind jedoch nicht für alle Wasserstoff- oder Kohlenstoffkerne gleich, sie hängen von der chemischen Umgebung ab, die jeden Kern umgibt. Dies liegt daran, dass die Elektronen, die jeden Kern umgeben, ein Magnetfeld erzeugen, das dem angelegten entgegengesetzt ist. Man sagt, dass die Kerne abgeschirmt sind, wobei σ die Abschirmkonstante ist.

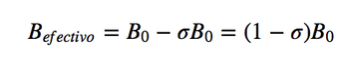
Bef ist das auf das Proton wirkende Nettomagnetfeld; B0 ist das angelegte Magnetfeld; σ ist die Abschirmungskonstante, unabhängig vom angelegten Feld. Unter dieser neuen Situation, bei der die Kerne durch die sie umgebende elektronische Dichte abgeschirmt sind, wird die Resonanzfrequenz

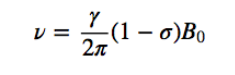
Kerne mit unterschiedlichen chemischen Umgebungen haben eine unterschiedliche Abschirmkonstante und erzeugen unterschiedliche Signale im NMR-Spektrum.

Ethanolspektrum:

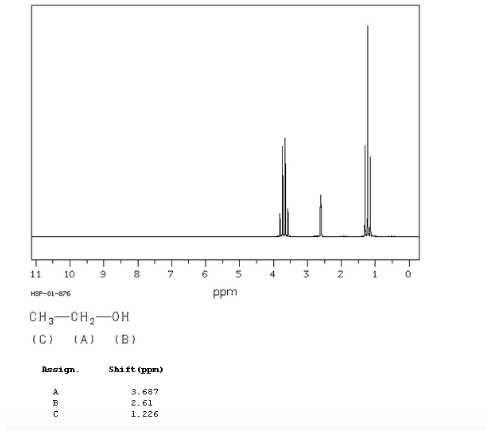
Im NMR-Spektrum von Ethanol werden aufgrund der Existenz von 3 Arten von Wasserstoffatomen mit unterschiedlichen chemischen Umgebungen drei verschiedene Signale beobachtet. Wasserstoff A ist aufgrund des Vorhandenseins von Sauerstoff (elektronegatives Atom, das Elektronendichte entfernt) unabgeschirmter als C. Die chemische Umgebung von Wasserstoff B, direkt an Sauerstoff gebunden, ist ebenfalls anders und schwingt mit einer anderen Frequenz als die vorherigen.

chemische Verschiebung

Signale im NMR-Spektrum werden auf einer vom angelegten Magnetfeld unabhängigen Skala gemessen, die als chemische Verschiebung bezeichnet und durch den Buchstaben δ dargestellt wird. Unabhängig davon, bei welchem Magnetfeld das Spektralfotometer arbeitet, werden die Signale einer chemischen Verbindung immer bei denselben Werten von δ erhalten:

Verschiebungstabelle:

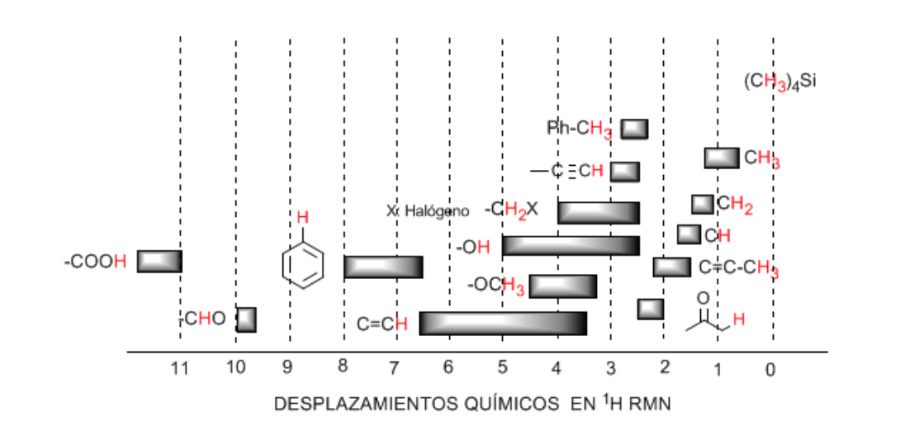
An aliphatischen Ketten befindliche Wasserstoffe weisen δ-Werte nahe 1 auf. Diese nehmen leicht zu, wenn von primären zu sekundären oder tertiären Kohlenstoffen übergegangen wird.

Die allylischen Wasserstoffatome liegen zwischen 1,5 und 2,1.

Alpha-Wasserstoffe in Bezug auf Carbonyle und Säurederivate liegen zwischen 2 und 2,5.

Die Benzylwasserstoffe zwischen 2,3 und 2,7.

Der Wasserstoff von terminalen Alkinen zwischen 2,5 und 3.

An Kohlenstoffe gebundene Wasserstoffe mit Halogenen zwischen 2,5 und 4, abhängig von der Elektronegativität des Halogens

Die Wasserstoffatome der Hydroxylgruppe zwischen 2,5 und 5. Sehr breites Spektrum durch Bildung von Wasserstoffbrückenbindungen.

An Sauerstoff vom Ethertyp gebundene Kohlenstoffwasserstoffe zwischen 3,3 und 4,5.

Olefinische Wasserstoffatome zwischen 3,5 und 6,5.

An aromatische Systeme gebundene Wasserstoffe zwischen 6,5 und 8.

Aldehydwasserstoff 9,5-10

Wasserstoff aus der Carbonsäuregruppe über 11.

Die elektronegativen Gruppen entschirmen die Kerne:

Elektronegative Substituenten entfernen die Elektronendichte, heben die Abschirmung der Wasserstoffatome auf und verschieben das Signal zu hohen δ-Werten.

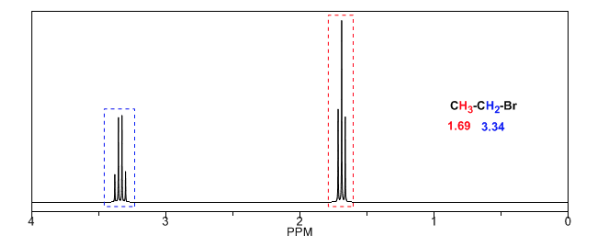
In der folgenden Tabelle sehen Sie den Einfluss verschiedener Atome auf das Signal der Methylwasserstoffe.

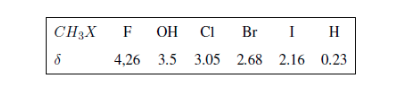
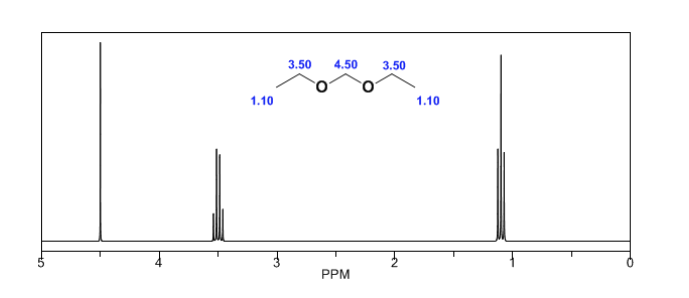
In den folgenden Spektren können die oben erwähnten Effekte auf chemische Verschiebungen beobachtet werden.

Magnetische Anisotropie:

Die Protonen in der Nähe von Doppelbindungen und aromatischen Ringen sind aufgrund des durch die elektronischen Ströme dieser Systeme induzierten Magnetfelds besonders ungeschirmt. Das induzierte Feld wird zum angelegten addiert, wodurch eine größere Verschiebung als erwartet entsteht.

Im folgenden Bild sehen wir die elektronische Zirkulation (fettgedruckte Kurven) und das induzierte Magnetfeld (gestrichelte Linien) für ein Alken und ein Carbonyl. Beobachten Sie, wie im Bereich des Protons das induzierte Magnetfeld die gleiche Richtung und Richtung hat wie das angelegte.

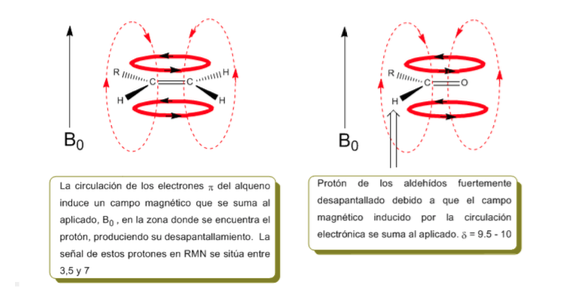
Eine ähnliche Situation wird im Fall von Benzol beobachtet. In Alkinen induziert die elektronische Zirkulation jedoch ein Magnetfeld, das dem im Protonenbereich angelegten entgegengesetzt ist. Die acetylenischen Wasserstoffatome werden mit Signalen im NMR-Spektrum bei geringen Offsets abgeschirmt.

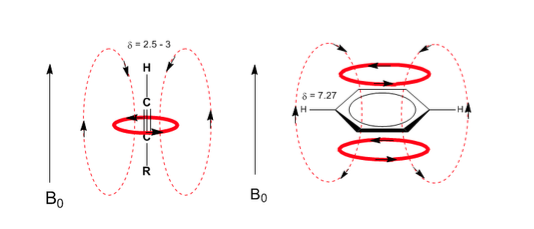
Beobachten Sie, wie die induzierten Felder die Verschiebungen des olefinischen Protons erheblich erhöhen, wobei auch die allylischen Positionen beeinflusst werden.

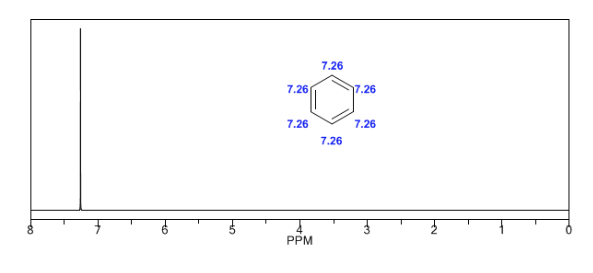
Die aromatischen Wasserstoffatome sind aufgrund des durch die Ringströme induzierten Feldes stark ungeschirmt.

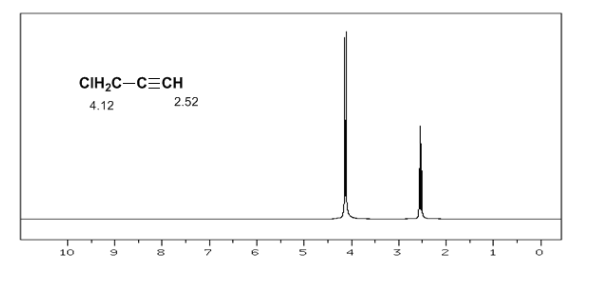
Der acetylenische Wasserstoff hat eine geringe Verschiebung, weil die Ströme ein Magnetfeld erzeugen, das dem angelegten entgegengesetzt ist.

Die häufigsten sauren Wasserstoffverschiebungen in organischen Molekülen sind:

• ·Carbonsäuren (RCOOH) δ= 10 - 12 ppm
• ·Amine (R−NH2) δ= 0,5 - 5 ppm
• Amide (RCONH2) δ= 5-8 ppm
• ·Alkohole (ROH) δ= 0,5 - 5 ppm
• Phenole (Ph-OH) δ= 4 - 7 ppm

Spin-Spin-Kopplung:

Die Strukturinformationen der NMR stammen aus zwei Faktoren: den unterschiedlichen beobachteten Verschiebungen in Abhängigkeit von der chemischen Umgebung, die das Proton umgibt, und der Kopplung zwischen den Spins benachbarter Protonen, die die Aufspaltung der Signale bewirkt.

Obwohl einige Signale im Spektrum einzelne Peaks sind, ist es üblich, Signale zu finden, die aus mehreren sehr nahen Peaks bestehen, die mit der folgenden Notation benannt werden: Singulett (s), Dublett (d), Triplett (t), Quadruplett (c) , Quintole (q), Sextole (sx) und Septole (sp) werden komplexe Signale als Multipletts bezeichnet. Der Wert von δ dieser Signale wird ihrer Mitte zugeordnet, es sei denn, das Multiplett ist unregelmäßig, in welchem Fall das Intervall angezeigt wird.

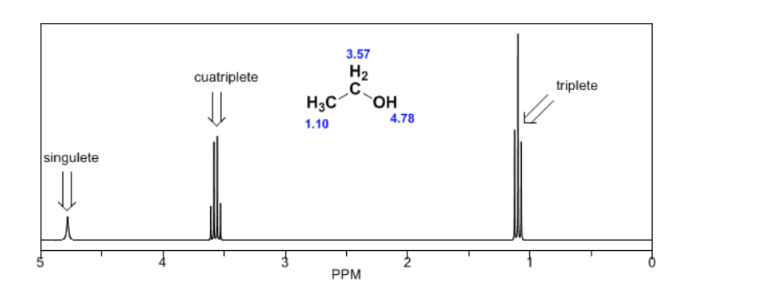
Im Spektrum von Ethanol ist ersichtlich, dass der Hydroxyl-Wasserstoff ein Singulett erzeugt, das Wasserstoffpaar an Kohlenstoff eins ein Quadruplett erzeugt und die drei Wasserstoffatome an Kohlenstoff zwei ein Triplett erzeugen.

Erklärung der Spin-Spin-Kopplung.

Um die Signalaufspaltung durch Spin-Spin-Kopplung zu verstehen, untersuchen wir das Spektrum von 1,1-Dichlor-2,2-diphenylethan ( Cl 2 CH a CH b Ph 2 ).

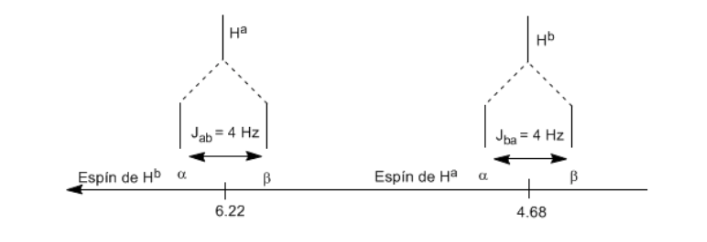
Das einem Magnetfeld B0 ausgesetzte Proton Ha erzeugt ein Signal bei δa=6,22 ppm. Das Hb-Proton erzeugt jedoch ein kleines Magnetfeld, das das Ha-Proton beeinflusst.Bei etwa der Hälfte der Moleküle ist das Hb-Proton auf das angelegte Feld ausgerichtet (Alpha-Spin) und bei der anderen Hälfte ist es gegen das Feld ausgerichtet (Beta-Spin). . Wenn Hb einen Spin α hat, wird Ha einem etwas größeren Feld ausgesetzt und schwingt bei einer höheren Frequenz (etwas höheres δ) mit. Wenn Hb einen β-Spin hat, wird Ha einem etwas kleineren Feld ausgesetzt und schwingt bei einer niedrigeren Frequenz (etwas niedrigeres δ) mit, was die anfängliche Spitze in zwei Signale aufteilt, die durch einen Abstand von 4 Hz getrennt sind, der als Kopplungskonstante (J) bezeichnet wird. Dieselbe Überlegung kann für das Hb-Proton angestellt werden.

Schließlich diskutieren wir die Kopplung eines Protons mit drei äquivalenten Nachbarprotonen. In diesem Fall wird ein Signal beobachtet, das aus vier Peaks (Quadtriplet) besteht. Die zentralen Spitzen sind dreimal so intensiv wie die äußersten Spitzen.

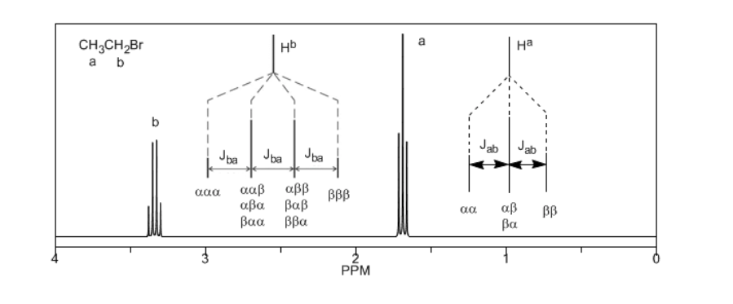
Regel N+1

Aus der obigen Diskussion kann abgeleitet werden, dass ein Proton ein Signal mit einer Anzahl von Peaks erzeugt, die um eine Einheit größer ist als die Anzahl benachbarter Wasserstoffatome. Im folgenden Bild sehen wir die Peaks, die von einem Hb-Wasserstoff erzeugt werden, wenn er mit einer Reihe von variablen Wasserstoffen gekoppelt wird

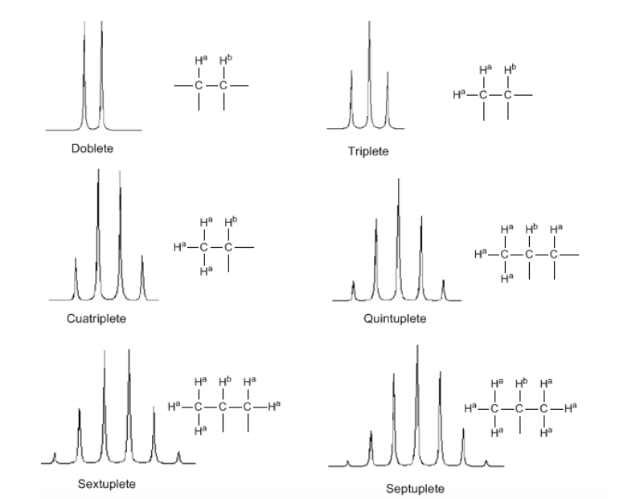
Die Intensität der Spitzen eines Signals wird durch das Pascalsche Dreieck (Tartaglia) angegeben:

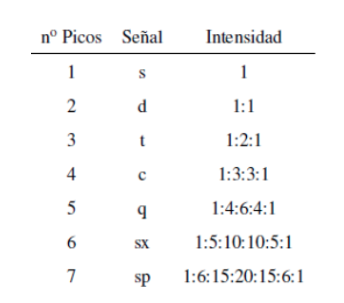
Bei der Anwendung der N+1-Regel sind zwei Überlegungen zu berücksichtigen:

• In Molekülen des Typs A-CHa2-CHb2-CHa2-A treten die Hb-Protonen als Quintuplet auf.
• In Molekülen des Typs A−CH2−CH2−A sind die vier Protonen äquivalent und ergeben ein Singulett.

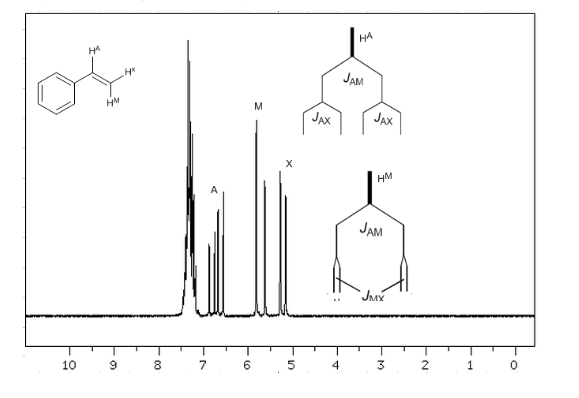
Kopplung dreier nicht äquivalenter Kerne:

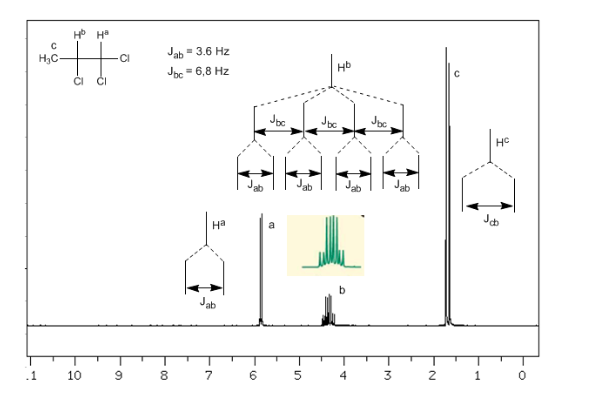
Berücksichtigt man, dass die Reihenfolge der Kopplungskonstanten in Alkenen Jtrans>Jcis>Jgeminal ist, sind die Kopplungsbäume für die Wasserstoffatome Ha und HM die im Spektrum angegebenen. Könnten Sie den Baum für Hx zeichnen?

13C Kernspinresonanz

Die kernmagnetische Resonanz von 13C ist komplementär zu der von 1H. Die letztgenannte Technik wird verwendet, um die Struktur des Kohlenstoffgerüsts durch Beobachtung der magnetischen Umgebung von Wasserstoffatomen abzuleiten, während die 13C-NMR-Spektroskopie die magnetische Umgebung von Kohlenstoffatomen bestimmt.

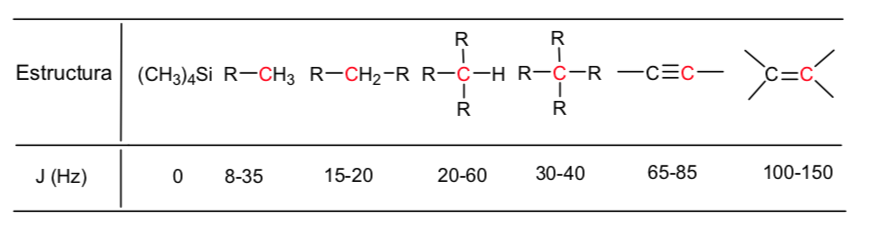
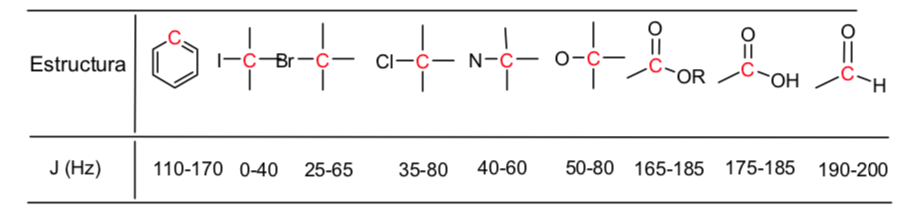
Empfohlene Referenzen zur Erweiterung der Suche:

1. Aga Fano SA Emissionsspektroskopie. (Abgerufen am 10. September 2007). http://hiq.aga.com.co/International/Web/LG/CO/likelgspgco.nsf/DocByAlias/anal_icp .

2. Alonso, P. et al. Chemie Cou..Ed. McGraw-Hill. 1990.

3. Álvarez Jiménez, MD und Gómez del Río, MI Didaktischer Leitfaden Analytische Chemie II. UNED. 1999.

4. Ankünfte Jimeno Siro; Burriel Barcelona Fernando; Hernández Mendez Jesus; Lucena Graf Felipe. Qualitative Analytische Chemie. ISBN: 8497321405. ISB. 2006.

5. Ayres, Gilbert H. Quantitative chemische Analyse. Editionen des Schlosses, 4. Aufl . ISBN: 8421902806. 1981.

6. Bermejo Barrera. M del Pilar. Allgemeine, quantitative und instrumentelle analytische Chemie. Redaktion Paraninfo. 7. Auflage. ISBN: 8428318093. 1990.

7. Blanco, M., Cerdá, V. und Sanz Medel, A., Analytical Atomic Spectroscopy, University Publications Autonom von Barcelona. 1990.

8. Brode. RW, Chemische Spektroskopie, New York 1952.

9. Burriel, MF, Lucena, CF. Quantitative Analytische Chemie. Revolutionäre Ausgabe. Havanna.1978.

10. Burriel, F. Qualitative Analytische Chemie. Redaktion Paraninfo. ISBN: 8497321405. S. 1072. , 2003.