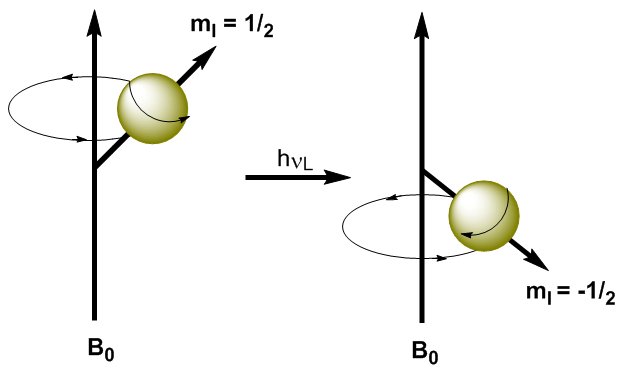
By applying electromagnetic radiation of suitable frequency (radio waves) it is possible to promote the nuclei from the lower energy level ($m_I=1/2$) to the higher energy level ($m_I=-1/2$). When electromagnetic radiation and the precession of the nucleus enter into resonance, absorption occurs. We can calculate the resonant frequency (Larmor frequency) using Planck's equation. \begin{equation}\label{ec7} \Delta E = h\nu_L \end{equation} Substituting the difference in energy for the equation (\ref{ec7}) \begin{equation}\label{ec8} \gamma\ hbar B_0=h\nu_L \end{equation} Solving for the Larmor Frequency \begin{equation}\label{ec10} \nu_L=\frac{\gamma}{2\pi}B_0 \end{equation} As can be seen in the equation (\ref{ec10}) the frequency at which the transition occurs depends on the applied magnetic field. The increase in the magnetic field produces an increase in the energy difference between the spin levels, so a higher frequency radiation is required to produce the transition.