Resonancia magnética nuclear
Las técnicas de Resonancia Magnética Nuclear (RMN) son un instrumento indispensable para la química así como para otras ramas de la Ciencia. Con la espectroscopia de RMN se pueden identificar moléculas (espectro Figura a), determinar su estructura o estudiar procesos dinámicos. Por ejemplo, ha sido clave en la determinación de la estructura de proteínas en disolución y, por otro lado, las técnicas de imagen de RMN son una herramienta indispensable en el diagnostico en medicina, como se ilustra en la (Figura b).
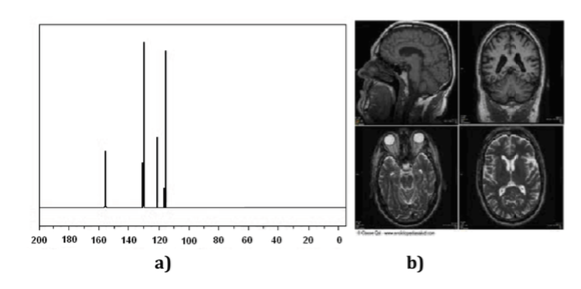
La RMN se sustenta en tres elementos:
a) El carácter magnético de los núcleos de las moléculas en estudio:
Muchos núcleos atómicos, debido al espín nuclear, presentan características magnéticas. En cierta manera se puede considerar que los núcleos se comportan como pequeños imanes.
b)La aplicación de un campo magnético intenso:
Cuando las moléculas en estudio están inmersas en un campo magnético, los niveles nucleares se desdoblan en varios niveles de energía. Cada uno de los niveles de energía que aparecen corresponden a diferentes orientaciones de los espines de los núcleos (pequeños imanes) respecto al campo magnético.
c) La iluminación de la muestra con radiación electromagnética:
Como en otras técnicas espectroscópicas la iluminación de la muestra con la frecuencia adecuada de radiación hará que los núcleos pasen de un nivel a otro. La frecuencia de la radiación necesaria para producir este salto de nivel, dependerá del tipo de núcleo, del entorno químico de éste, del tipo de núcleos presentes en sus cercanías y del campo externo aplicado. A lo largo de este tema se estudiarán los fundamentos físicos de esta técnica, y se explicarán las técnicas experimentales que permiten obtener los espectros, analizando, asimismo, las causas que hacen diferentes los espectros de las diversas moléculas.
Conceptos basicos de RMN:
Espín nuclear y momento angular de espín nuclear
Los núcleos atómicos están formados por protones y neutrones. Ambos nucleones tienen momento angular orbital y momento angular de espín (tanto protones como neutrones tienen espín 1/2). La resultante de la suma vectorial de todos los momentos (orbitales y de espín) de todos los protones y neutrones del núcleo da como resultado el momento angular de espín nuclear y se simboliza por I y sus unidades son J s. Según la mecánica cuántica, el módulo del momento angular de espín nuclear, |I|, está cuantizado, con un valor I(I+1)hdonde I es el número cuántico de espín nuclear o espín nuclear y ħ es h/2p(que en el sistema internacional vale 1,05457·10‐34J·s). El valor de I es una característica fija de cada tipo de núcleo atómico y puede tomar unvalor entero o semientero (0,1, 2, 3,… ½ , 3/2 , 5/2….).
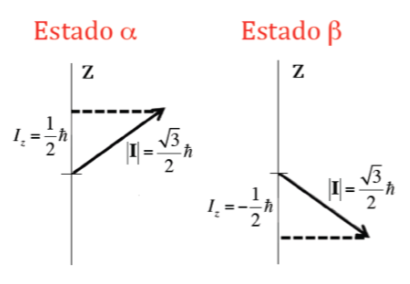
Además del módulo, también es importante conocer la componente del momento angular sobre el eje z, Iz. Esta puede tomar, asimismo, valores cuantizados dados por la expresión mIh donde mI es el número cuántico asociado a la componente z del momento angular de espín nuclear y que puede tomar los siguientes valores: –I, (‐I+1), ... , (I‐1), I. Así para un núcleo determinado, con un valor de I, existen (2I+1) orientaciones del momento angular de espín nuclear. Por ejemplo, considérese el núcleo atómico del isótopo más común del átomo de hidrogeno, 1H, que está formado por un protón y se sabe que su espín nuclear, I, es 1/2, y por tanto mI podrá tomar dos valores +1/2 y ‐1/2 (en RMN se suele denominar al isótopo 1H como protón). El protón tiene pues dos posibles estados nucleares uno denominado aconmI=+1/2 y otro bcon mI=‐1/2. En la Figura de mas adelante se muestran las dos posibles orientaciones del momento angular de espín nuclear correspondientes a los estados ayb, que energéticamente son equivalentes.
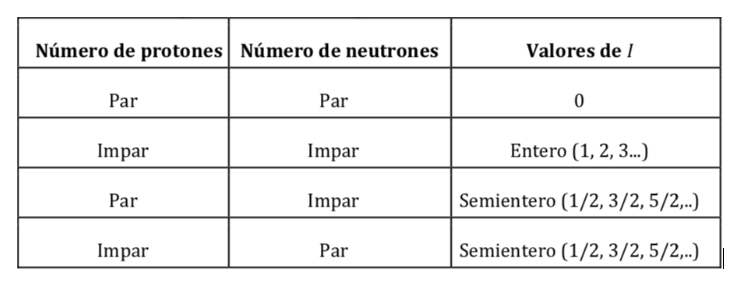
Valores de I según el número de protones y de neutrones del núcleo :
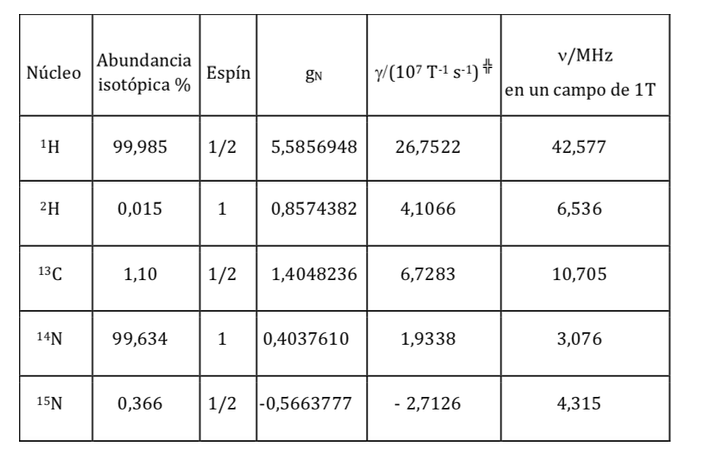
Propiedades magnéticas de diversos núcleos:
Momento dipolar magnético nuclear (magnetón nuclear, relación giromagnética ):
Así como el electrón tiene un momento dipolar magnético, algunos núcleos atómicos, pero no todos, presentan un momento dipolar magnético. Como se ha indicado, los núcleos se comportan como pequeños imanes, siendo el origen de este carácter magnético el momento angular del espín nuclear. El momento angular de espín nuclear, I, origina un momento dipolar magnético nuclear mI que viene dado por:
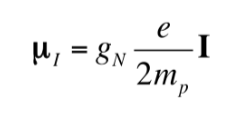
donde gN es el factor g nuclear. Obsérvese que en esta expresión se utiliza por definición la masa y carga del protón (mp y e), en lugar de la masa y la carga del núcleo en cuestión. Las diferencias de un núcleo a otro se engloban en el factor gN nuclear. El valor de gN no puede obtenerse teóricamente, por lo que se determina experimentalmente. Las unidades de mI son J T‐1
La relación entre mI eI, también se puede expresar de la siguiente forma:
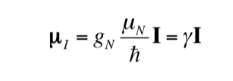
con
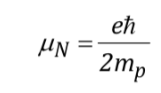
siendo una constante con un valor de 5,050 10‐27J T‐1 denominadamagnetón nuclear y ges la relación giromagnética (T‐1s‐1).En las tablas anteriores ya se mostraron valores de estas magnitudes para algunos isótopos. Aunque en la mayoría de los casos mI e I tienen el mismo sentido, a veces es opuesto, como se deduce de los valores negativos del factor gN y de gpara el isótopo 15N, por ejemplo.
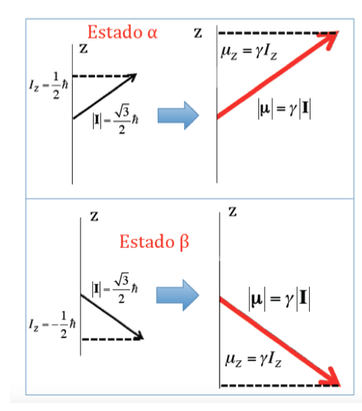
En el caso del protón donde se habían visto dos posibles orientaciones del momento angular se tendrán dos posibles orientaciones del momento magnético dipolar, como se ilustra en la siguiente figura , siendo ambas orientaciones energéticamente equivalentes, ya que la elección de una dirección z es arbitraria.
Energía de interacción del campo magnético con el momento magnético nuclear:
Si se introduce una molécula dentro de un campo magnético, con densidad de flujo o campo magnético B, el momento magnético dipolar de cada uno de sus núcleos interaccionará con él, como se ilustra en la siguiente figura , viniendo expresada la energía de la interacción por:
![]()
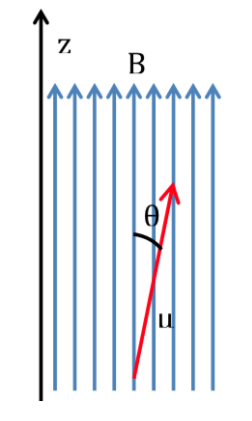
Según la física clásica, todas las orientaciones de un dipolo magnético dentro de un campo magnético son permitidas y por tanto qpuede tomar cualquier valor entre 0 y 180o. Dependiendo de la orientación del dipolo la energía será mayor o menor:
La interacción más favorable se da cuando ambas magnitudes tienen el mismo sentido: q=0 y por tanto cos q=1 y :
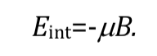
Sin embargo, según la mecánica cuántica, no todas las orientaciones del dipolo magnético nuclear están permitidas, las orientaciones están cuantizadas y sólo son posibles unos determinados valores de q. Hay tantas orientaciones permitidas como valores de Iz o de mI (‐I, ‐I+1,..., I‐1, I) es decir 2I+1 orientaciones. Evidentemente el número de orientaciones del momento dipolar varía con el tipo de núcleo atómico. Para poder definir las orientaciones se toma la dirección y sentido del campo B como referencia del eje Z.
Así la energía de interacción del campo magnético exterior B y el dipolo nuclear vendrá dada por: j
Frecuencia de Langmor
Si sobre el núcleo actúa un campo magnético externo de intensidad B, el dipolo magnético nuclear experimenta un par de fuerzas como se muestra en la siguiente formula dado por:
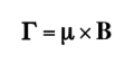
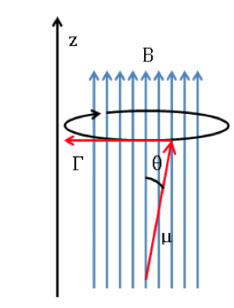
que tiende a alinear el dipolo con el campo magnético. Como el dipolo magnético no puede alinearse con el campo magnético, el sistema no es capaz de disipar esta energía y describe un movimiento de precesión, denominado precesión de Larmor, en
torno a la dirección del campo aplicado. La frecuencia de esta precesión se llama frecuencia de Larmor, con un valor:
Esquema de langmor :
Espectroscopia de RMN
La clave de cualquier técnica espectroscópica se basa en la posibilidad de que la molécula en estudio pueda estar en más de un nivel de energía, de tal forma, que haciendo incidir radiación electromagnética (r.e.m) de la frecuencia adecuada, se pueda pasar a nuestro sistema (molécula) de un nivel energético a otro. Como se ha visto en el apartado anterior, el núcleo de un protón, inmerso en un campo magnético, puede ocupar dos niveles diferentes asociados al espín nuclear, por tanto haciendo incidir un haz de r.e.m de la frecuencia adecuada sobre un núcleo de 1H que esté ocupando el nivel inferior, se le puede pasar al nivel superior. Este tipo de transiciones es lo que da lugar a la Espectroscopia de Resonancia Magnética Nuclear (RMN). A partir de ahora nos centraremos en el caso del protón 1H, por ser la espectroscopia más empleada, aunque todo lo que se indique es aplicable a otros núcleos. De hecho, cada vez se utiliza más variedad de núcleos.
Frecuencia de resonancia:
La frecuencia que provoca la transición se obtiene aplicando la condición de resonancia:
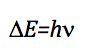
Como la diferencia de energía entre dos niveles consecutivos es:
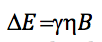
igualando ambas expresiones y despejando n:
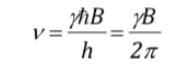
que, como se puede observar, coincide con la frecuencia de precesión de Larmor.
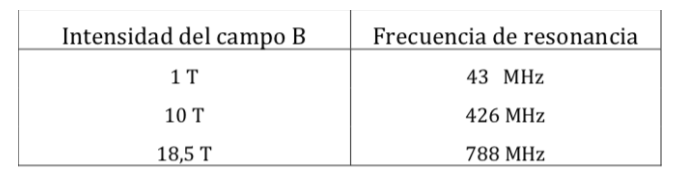
Frecuencias de resonancia de RMN de protón para diversas intensidades de campo :
Reglas de selección :
Las reglas de selección que se estudiaron en otras espectroscopias corresponden a la interacción del dipolo eléctrico con el campo eléctrico de la radiación. En cambio en RMN la interacción se produce entre el dipolo magnético del núcleo y el campo magnético variable de la radiación. Para determinar las reglas de selección, se debe recordar la expresión general que determina la probabilidad de paso entre dos estados es:
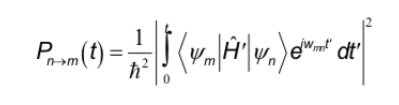
El hamiltoniano, en este caso, es el producto del operador del campo magnético oscilante de la radiación por el operador del momento dipolar del núcleo.
![]()
Se puede demostrar que para que haya una transición entre dos niveles la correspondiente regla de selección es:
mI=±1
Intensidad de la señal (población de los niveles ):
La intensidad de la señal está directamente relacionada con la población de los niveles involucrados en la transición. Según la ley de distribución de Boltzman, para un sistema de dos niveles, como el protón, el cociente de la población del nivel superior, Nb, y la población del nivel inferior Na, viene dado por:
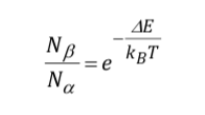
Descripción de los equipos de RMN :
¿Qué procedimiento experimental se utiliza par obtener el espectro? Generalmente en espectroscopia se varía la frecuencia de la radiación incidente, hasta que se observa absorción. Sin embargo, en espectroscopia RMN se tiene además la opción de mantener fija la frecuencia de la radiación y variar el espaciado entre los niveles, variando la magnitud del campo aplicado B hasta que se observe absorción. En la siguiente figura donde se presenta un esquema de un equipo de RMN. La muestra se coloca en un tubo, que, algunas veces, se gira rápidamente para ganar homogeneización en la señal, aunque actualmente está en discusión el uso del giro, pues puede introducir errores. El tubo, a su vez, está situado entre dos polos magnéticos que son los que generan el campo magnético. Hay un emisor y un receptor de radiofrecuencia. La señal del emisor puede ser controlada para hacer un barrido de frecuencias. Con las bobinas de barrido se puede controlar un barrido del campo. Los equipos actuales de RMN ya casi no emplean :
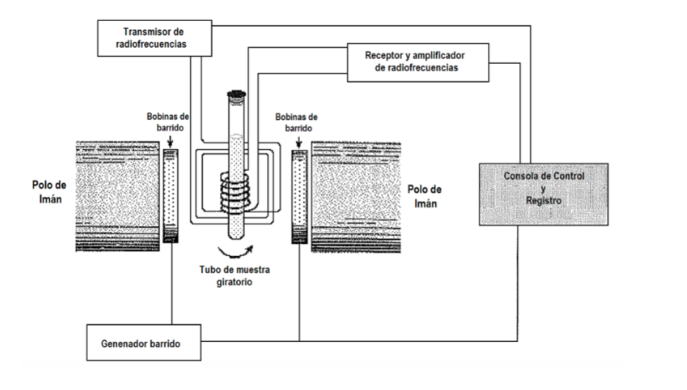
los procedimientos anteriores, sino que se basan en la utilización de técnicas de transformadas de Fourier. B se mantiene fijo y la muestra se ilumina con un pulso de radiofrecuencias de duración determinada y de alta potencia con frecuencia nrad, un valor fijo en el intervalo de frecuencias de RMN del tipo de núcleo que se esté estudiando. El pulso dura varios microsegundos, debido a lo cual, se puede demostrar matemáticamente por una técnica llamada análisis de Fourier, que el pulso de radiofrecuencias es equivalente a un intervalo de frecuencias ∆nen torno a nrad y excita todas las posibles resonancias de RMN. La señal observada en el detector contendrá todas las frecuencias de resonancia y se analiza con un ordenador utilizando técnicas de transformada de Fourier. Este procedimiento permite muy alta resolución y trabajar con núcleos que con los procedimientos anteriores tenían señales muy débiles.
Apantallamiento nuclear:
En resonancia Magnética se utilizan núcleos con momento angular de espín distinto de cero, como pueden ser 1H y 13C. Sin embargo, las frecuencias de resonancia no son iguales para todos los núcleos de hidrógeno o de carbono, dependen del entorno químico que rodea cada núcleo. Esto se debe a que los electrones que rodean cada núcleo generan un campo magnético que se opone al aplicado, se dice que los núcleos están apantallados, siendo σ la constante de apantallamiento.
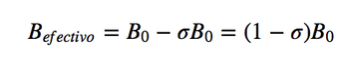
Bef es el campo magnético neto que actúa sobre el protón; B0 es el campo magnético aplicado; σ es la constante de apantallamiento, independiente del campo aplicado. Bajo esta nueva situación, con los núcleos apantallados por la densidad electrónica que los rodea, la frecuencia de resonancia pasa a ser
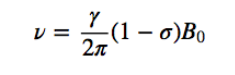
Los núcleos con distinto entorno químico presentan una constante de apantallamiento diferente, generando diferentes señales en el espectro de RMN.
Espectro del etanol:
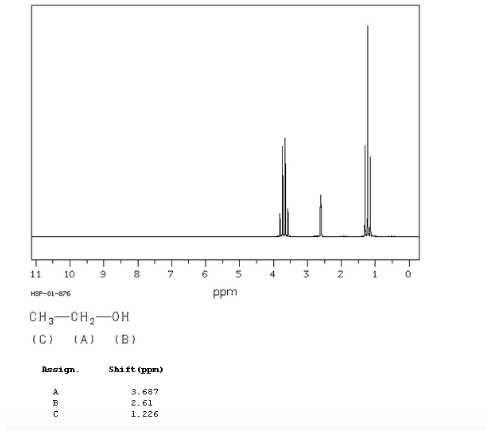
En el espectro de RMN del etanol se observan tres señales diferentes, debido a la existencia de 3 tipos de hidrógenos con distinto entorno químico. Los hidrógenos A están más desapantallados que los C debido a la presencia del oxígeno (átomo electonegativo que retira densidad electrónica). El entorno químico del hidrógeno B, unido directamente al oxígeno, también es diferente resonando a una frecuencia distinta a los anteriores.
Desplazamiento quimico
Las señales del espectro de RMN se miden en una escala independiente del campo magnético aplicado, llamada desplazamiento químico y representada por la letra δ. Independientemente del campo magnético al que trabaje el espectrofotómetro, las señales de un compuesto químico se obtienen siempre a los mismos valores de δ:

Tabla de desplazamientos:
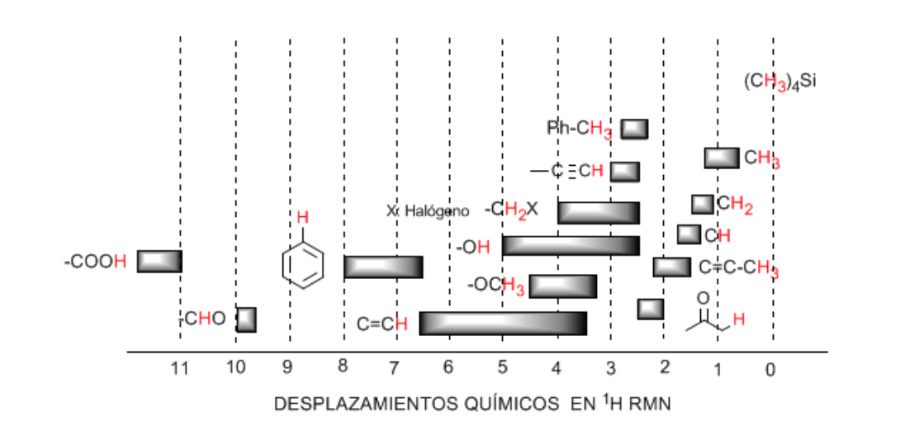
Los hidrógenos situados sobre cadenas alifáticas presentan valores de δ próximos a 1. Aunmentando ligeramente al pasar de carbonos primarios a secundarios o terciarios.
Los hidrógenos alílicos se localizan entre 1,5 y 2,1.
Los hidrógenos alfa respecto a carbonilos y derivados de ácido se sitúan entre 2 y 2,5.
Los hidrógenos bencílicos entre 2,3 y 2,7.
El hidrógeno de alquinos terminales entre 2,5 y 3.
Hidrógenos unidos a carbonos con halógenos entre 2,5 y 4 dependiendo de la electronegatividad del halógeno
Los hidrógenos del grupo hidroxilo entre 2,5 y 5. Rango muy amplio debido a la formación de puentes de hidrógeno.
Hidrógenos de carbonos unidos a oxígeno tipo éter entre 3,3 y 4,5.
Hidrógenos olefínicos entre 3,5 y 6,5.
Hidrógenos unidos a sistemas aromáticos entre 6,5 y 8.
Hidrógeno de aldehídos 9,5-10
Hidrógeno del grupo ácido carboxílico por encima de 11.
Los grupos electronegativos desapantallan los nucleos :
Los sustituyentes electronegativos retiran densidad electrónica, desapantallando los hidrógenos y desplazan la señal hacia valores altos de δ.
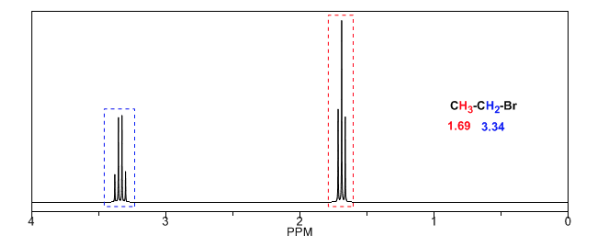
En la siguiente tabla puede verse la influencia de diferentes átomos sobre la señal de los hidrógenos del metilo.
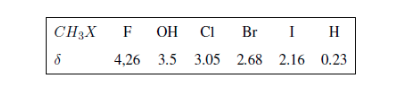
En los siguientes espectros puede observarse los efectos comentados anteriormente sobre los desplazamientos químicos.
Anisotropia magnetica:
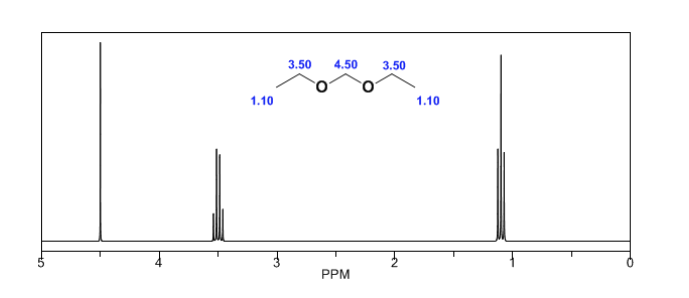
Los protones próximos a dobles enlaces y anillos aromáticos están especialmente desapantallados debido al campo magnético inducido por las corrientes electrónicas de estos sistemas. El campo inducido se suma al aplicado, produciendo un desplazamiento superior al esperado.
En la siguiente imagen podemos ver la cirulación electrónica (curvas en negrita) y el campo magnético inducido (lineas a trazos) para un alqueno y un carbonilo. Obsérvese como en la región del protón el campo magnético inducido tiene identica dirección y sentido que el aplicado.
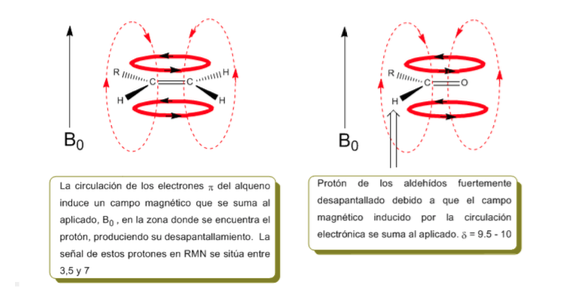
En el caso del benceno se observa una situación análoga. Sin embargo, en los alquinos la circulación electrónica induce un campo magnético que se opone al aplicado en la zona del protón. Los hidrógenos acetilénicos están apantallados con señales en el espectro de RMN a desplazamientos bajos.
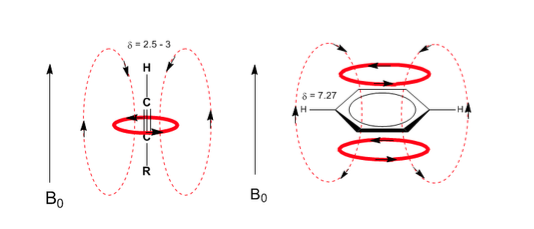
Obsérvese como los campos inducidos aumentan considerablemente los deplazamientos del protón olefínico, viéndose también afectadas las posiciones alílicas.
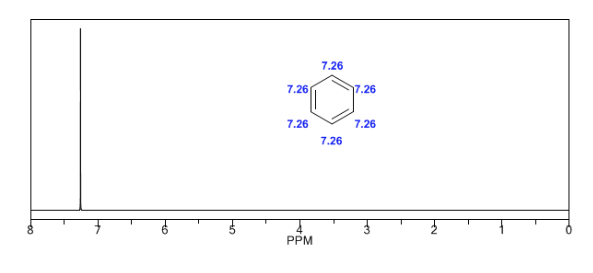
Los hidrógenos aromáticos están fuertemente desapantallados debido al campo inducido por las corrientes del anillo.
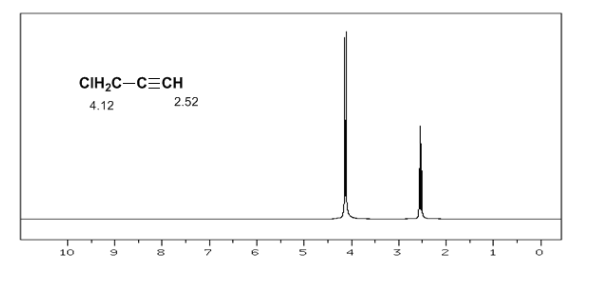
El hidrógeno acetilénico presenta un desplazamiento bajo, debido a que las corrientes producen un campo magnético que se opone al aplicado.
Los desplazamientos hidrógenos ácidos más comunes en las moléculas orgánicas son:
- ·Ácidos carboxílicos (RCOOH) δ= 10 - 12 ppm
- ·Aminas (R−NH2) δ= 0.5 - 5 ppm
- ·Amidas (RCONH2) δ= 5-8 ppm
- ·Alcoholes (ROH) δ= 0.5 - 5 ppm
- ·Fenoles (Ph-OH) δ= 4 - 7 ppm
Acoplamiento espin-espin:
La información estructural del RMN deriva de dos factores: los diferentes desplazamientos observados dependiendo del ambiente químico que rodea al protón y del acoplamiento entre los espines de protones próximos, que produce el desdoblamiento de las señales.
Aunque algunas señales del espectro son picos simples, es habitual encontrar señales compuestas por varios picos muy próximos, que se nombran con la siguiente notación: singulete (s), doblete (d), triplete (t), cuatriplete (c), quintuplete (q), sextuplete (sx) y septuplete (sp), señales complejas se las designa como multipletes. El valor de δ de estas señales se asigna al centro de las mismas, salvo que el multiplete sea irregular en cuyo caso se indica el intervalo.
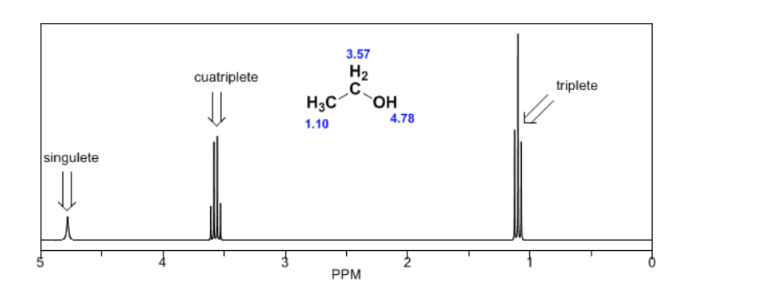
En el espectro del etanol puede observarse que el hidrógeno hidroxílico produce un singulete, la pareja de hidrógenos del carbono uno dan lugar a un cuatriplete y los tres hidrógenos del carbono dos producen un triplete.
Explicación del acoplamiento espín-espín.
Para comprender el desdoblamiento de las señales debido al acoplamiento espín-espín vamos a estudiar el espectro del 1,1-dicloro-2,2-difeniletano (Cl2CHaCHbPh2).
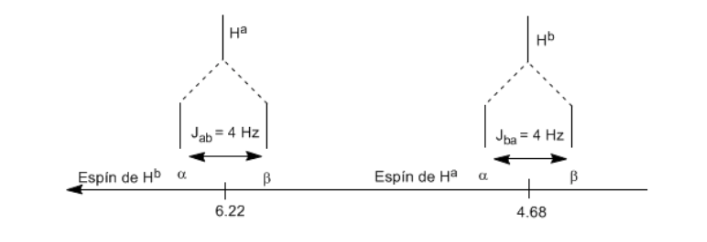
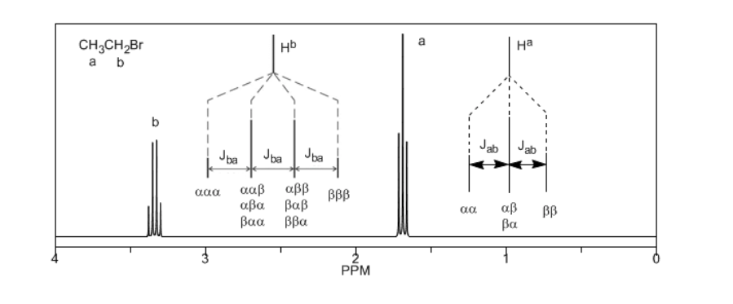
El proton Ha sometido a un campo magnético B0 produce una señal a δa=6,22ppm. Sin embargo, el protón Hb genera un pequeño campo magnético que afecta al protón Ha. Aproximadamente la mitad de las moléculas tienen el protón Hb alineado con el campo aplicado (espín alfa) y la otra mitad lo tienen orientado en contra del campo (espín beta). Cuando Hb tiene espín α, Ha se ve sometido a un campo ligeramente mayor y resuena a una mayor frecuencia (δ ligeramente mayor). Cuando Hb tiene espín β, Ha se ve sometido a un campo ligeramente menor y resuena a menor frecuencia (δ ligéramente menor), lo cual produce el desdoblemiento del pico inicial en dos señales separados por una distancia de 4 Hz, llamada constante de acoplamiento (J). Este mismo razonamiento se puede realizar para el proton Hb.
Por último, discutiremos el acoplamiento de un protón con tres protones vecinos equivalentes. En este caso se observa una señal formada por cuatro picos (cuatriplete). Los picos centrales poseen el triple de intensidad que los picos de los extremos.
Regla N+1
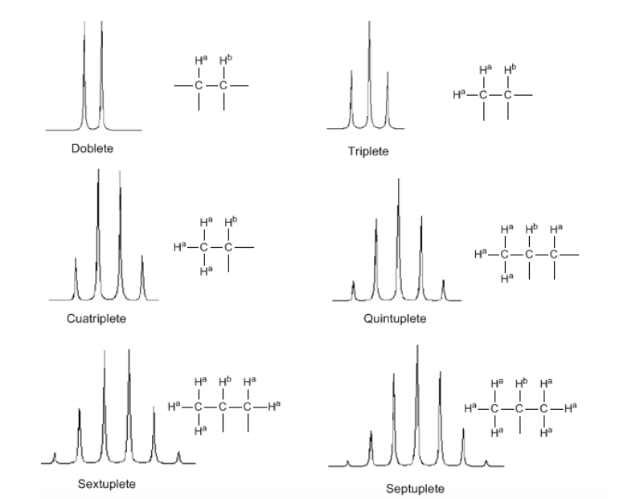
De la discusión anterior puede deducirse que un protón produce una señal con un número de picos una unidad superior al número de hidrógenos vecinos. En la siguiente imagen podemos observar los picos que produce un hidrógeno Hb al acoplarse con un número de hidrógenos variables
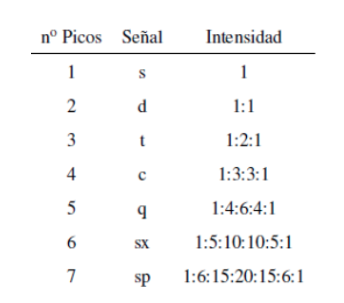
La intensidad de los picos de una señal vienen dados por el triángulo de Pascal (Tartaglia):
Deben tenerse en cuenta dos consideraciones al aplicar la regla N+1:
- En moléculas del tipo A−CHa2−CHb2−CHa2−Alos protones Hb aparecen como un quintuplete.
- En moléculas del tipo A−CH2−CH2−A, los cuatro protones son equivalentes y dan un singulete.
Acoplamiento de tres nucleos no equivalentes:
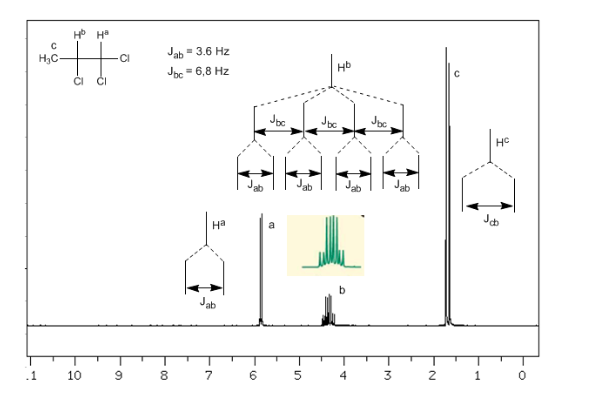
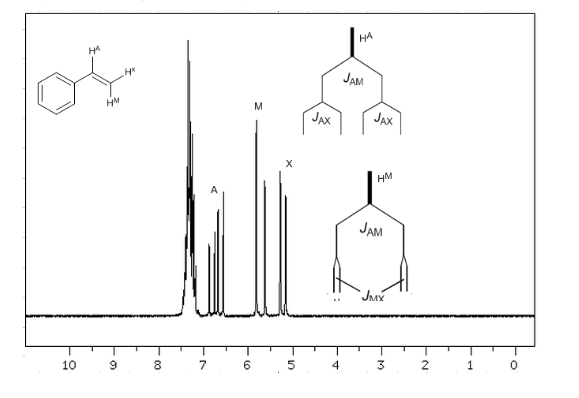
Teniendo en cuenta que el orden de constantes de acoplamiento en alquenos es Jtrans>Jcis>Jgeminal, los árboles de acoplamiento para los hidrógenos Ha y HM son los indicados en el espectro. ¿Serías capaz de dibujar el arbol para Hx?
Resonancia magnética nuclear de 13C
La resonancia magnética nuclear de 13C es complementaria a la de 1H. Esta última técnica se utiliza para deducir la estructura del esqueleto carbonado observando los entornos magnéticos de los átomos de hidrógeno, mientras que la espectroscopia de RMN de 13C determina el entorno magnético de los átomos de carbono.
Los desplazamientos químicos del carbono son de 15 a 20 veces mayores que los del hidrógeno debido a que el carbono está directamente unido a los átomos que resultan ser bien apantallantes o desapantallantes. Por ejemplo, el protón de un aldehído absorbe a 9.4 ppm en el espectro de 1H mientras que el carbono de carbonilo absorbe a 180 ppm en el espectro de 13C.
Además, las señales en el espectro de 13C son líneas verticales, es decir, no hay desdoblamientos de espín-espín. Esto se debe a que sólo el 1% de los átomos de carbono entran en resonancia, y por tanto, existe una probabilidad muy pequeña de que un núcleo de 13C esté adyacente a otro núcleo de 13C.
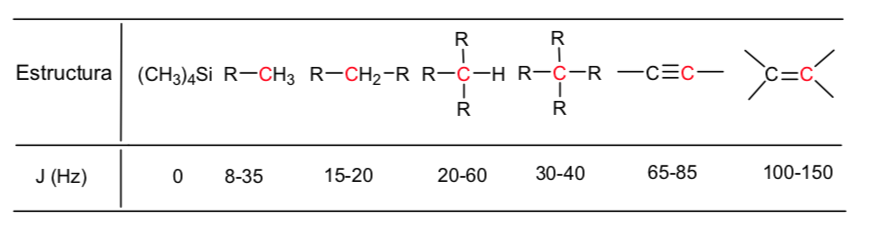
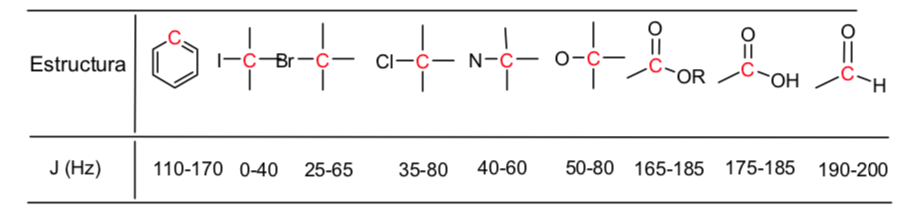
A continuación se da una tabla de valores aproximados de desplazamientos químicos en un espectro de resonancia magnética nuclear de 13C:
Referencias recomendadas para expandir la busqueda :
1. Aga Fano S.A. Espectroscopia de Emisión. (acceso 10 de septiembre del 2007).http://hiq.aga.com.co/International/Web/LG/CO/likelgspgco.nsf/DocByAlias/anal_icp.
2. Alonso, P. et al. quimicaCou..Ed. Mc Graw-Hill. 1990.
3. Álvarez Jiménez, M. D. y Gómez del Río, M. I. Guía didacticaQuímica Analítica II. UNED. 1999.
4. Arribas Jimeno Siro; Burriel Barcelo Fernando; Hernández Méndez Jesús; Lucena Conde Felipe. Química Analítica Cualitativa. ISBN: 8497321405. ISB. 2006.
5. Ayres, Gilbert H. Análisis Químico Cuantitativo. Ediciones del Castillo, 4ta ed. ISBN: 8421902806. 1981.
6. Bermejo Barrera. M del Pilar. Química analítica general, cuantitativa e instrumental. Editorial Paraninfo. 7ma Edición. ISBN: 8428318093. 1990.
7. Blanco, M., Cerdá, V. y Sanz Medel, A., Espectroscopia Atómica Analítica, Publicaciones de la universidadAutónoma de Barcelona. 1990.
8. Brode. R.W, Chemical spectroscopy, Nueva York 1952.
9. Burriel, M.F., Lucena, C.F.Química Analítica Cuantitativa. Edición Revolucionaria. La Habana.1978.
10. Burriel, F. Química Analítica Cualitativa. Editorial Paraninfo. ISBN: 8497321405. pp 1072. , 2003.
 ¿Te cuesta entender la Química Orgánica?
¿Te cuesta entender la Química Orgánica?