¿Te cuesta entender la Química Orgánica?
¿Te cuesta entender la Química Orgánica?
Cursos de Química Orgánica para los Grados en Química, Ingeniería Química, Biotecnología y Farmacia de las Universidades españolas.
Material específico para cada Universidad con teoría, ejercicios y exámenes resueltos en vídeo, creado por Germán Fernández. Soporte para dudas por WhatsApp. .
Más información en www.foroquimico.com
Si prefieres un curso de química orgánica tanto básica como avanzada te invito a acceder al canal: https://www.youtube.com/channel/UC_RiUaA2326jO9XozAA4q2g , en el que encontrarás más de 750 vídeos de teoría y ejercicios.
RESONANCIA MAGNÉTICA NUCLEAR (RMN)
- Detalles
- Germán Fernández
- RESONANCIA MAGNÉTICA NUCLEAR (RMN)
- Visto: 18067
Los núcleos atómicos rotan sobre sí mismos (espín) y presentan un momento angular que viene dado por la expresión \begin{equation}\label{ec1} L=\sqrt{I(I+1)}\hbar \end{equation} El momento angular depende del número cuántico I (número cuántico del momento angular o espín nuclear), que puede tomar diferentes valores dependiendo del tipo de núcleo, I=0, 1/2, 1, 3/2, 2, 5/2, 3,.....
El cálculo del número cuántico de espín para un núcleo se realiza sumando los espines de protones y neutrones desapareados. Por ejemplo, el hidrógeno tiene I=1/2, al estar formado por un sólo protón.
Los estados cuánticos de espín permitidos vienen dados por $m_I$, que toma los siguientes valores \begin{equation}\label{ec2} m_I=-I, -I+1, ...., I-1, I \end{equation} El número de valores que toma $m_I$ para un valor dado de I son $2I+1$. Así, para un núcleo con I=1/2 existen dos estados cuánticos posibles de espín dados por $m_I=-1/2, 1/2$. Un núcleo con I=1 tiene tres estados cuáticos de espín permitidos $m_I=-1, 0, +1$. En ausencia de campo magnético los estados cuánticos de espín están degenerados.
- Detalles
- Germán Fernández
- RESONANCIA MAGNÉTICA NUCLEAR (RMN)
- Visto: 17914
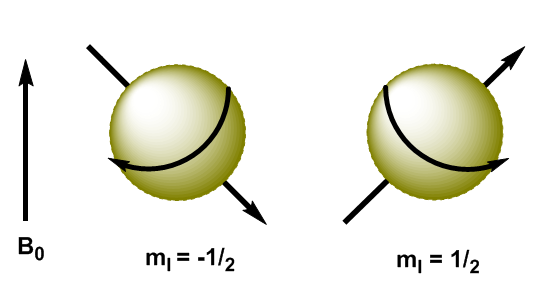
Los núcleos atómicos son partículas cargadas y su momento angular produce un momento magnético, representado por $\mu$ \begin{equation}\label{ec3} \mu=\gamma L = \gamma \sqrt{I(I+1)}\hbar \end{equation} donde $\gamma$ es la constante giromanética, característica de cada núcleo. Cuando aplicamos un campo magnético, $B_0$, a núcleos con I=1/2, los momentos magnéticos se orientan de forma que los núcleos con $m_I=1/2$ presentan su momento magnético alineado con el campo y los núcleos con $m_I=-1/2$ tienen su momento magnético opuesto al campo aplicado.
- Detalles
- Germán Fernández
- RESONANCIA MAGNÉTICA NUCLEAR (RMN)
- Visto: 14553
En mecánica cuántica el momento angular magnético en dirección z viene dado por $L_z=m_I\hbar$. El núcleo con $m_I=1/2$ tiene $L_z=1/2\hbar$, mientras que el núcleo con $m_I=-1/2$ tiene $L_z=-1/2\hbar$. El momento magnético en esta dirección es $\mu_z=\gamma L_z$.
Estas ecuaciones nos permiten determinar la energía de ambos niveles. \begin{equation}\label{ec4} E=-\mu_zB_0=-\gamma m_I\hbar B_0 \end{equation} Ahora podemos calcular la diferencia de energía entre ambos niveles \begin{equation}\label{ec6} \Delta E=-\gamma (-1/2)\hbar B_0 + \gamma 1/2\hbar B_0=\gamma\hbar B_0 \end{equation}
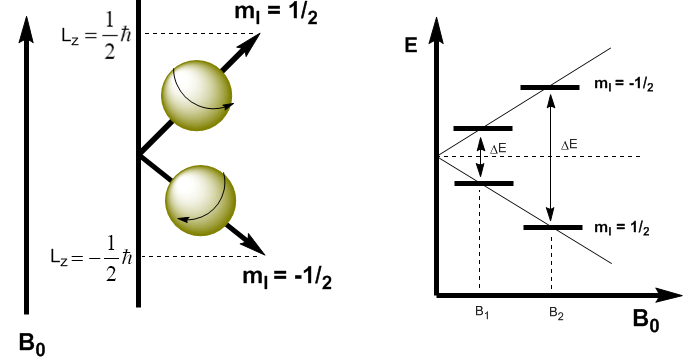
Como puede observarse en la ecuación (\ref{ec6}) la diferencia de energía depende del campo magnético aplicado. Si el campo magnético es bajo, $\Delta E$ es pequeño y la diferencia de población entre ambos niveles también es baja, lo que provoca un problema de sensibilidad. A campos magnéticos elevados tenemos una separación importante entre niveles lo que da lugar a una diferencia de población alta, obteniéndose una mayor sensibilidad.
- Detalles
- Germán Fernández
- RESONANCIA MAGNÉTICA NUCLEAR (RMN)
- Visto: 16801
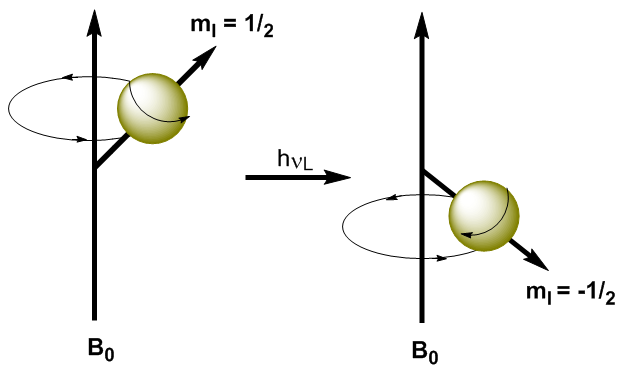
Al aplicar una radiación electromagnética de frecuencia adecuada (ondas de radio) se consigue promocionar los núcleos desde el nivel de energía inferior ($m_I=1/2$) al nivel de energía superior ($m_I=-1/2$). Cuando la radiación electromagnética y la precesión del núcleo entran en resonancia se produce la absorción. Podemos calcular la frecuencia de resonancia (frecuencia de Larmor) mediante la ecuación de Planck. \begin{equation}\label{ec7} \Delta E = h\nu_L \end{equation} Sustituyendo la diferencia de energía por la ecuación (\ref{ec7}) \begin{equation}\label{ec8} \gamma\hbar B_0=h\nu_L \end{equation} Despejando la Frecuencia Larmor \begin{equation}\label{ec10} \nu_L=\frac{\gamma}{2\pi}B_0 \end{equation} Como puede observarse en la ecuación (\ref{ec10}) la frecuencia a la que se produce la transición depende del campo magnético aplicado. El aumento en el campo magnético produce un aumento en la diferencia de energía entre los niveles de espín, por lo que se requiere una radiación de frecuencia mayor para poducir la transición.
- Detalles
- Germán Fernández
- RESONANCIA MAGNÉTICA NUCLEAR (RMN)
- Visto: 21568
En resonancia Magnética se utilizan núcleos con momento angular de espín distinto de cero, como pueden ser $^1H$ y $^{13}C$. Sin embargo, las frecuencias de resonancia no son iguales para todos los núcleos de hidrógeno o de carbono, dependen del entorno químico que rodea cada núcleo. Esto se debe a que los electrones que rodean cada núcleo generan un campo magnético que se opone al aplicado, se dice que los núcleos están apantallados, siendo $\sigma$ la constante de apantallamiento. \begin{equation}\label{ec11} B_{efectivo}=B_0-\sigma B_0=(1-\sigma)B_0 \end{equation} $B_{ef}$ es el campo magnético neto que actúa sobre el protón; $B_0$ es el campo magnético aplicado; $\sigma$ es la constante de apantallamiento, independiente del campo aplicado. Bajo esta nueva situación, con los núcleos apantallados por la densidad electrónica que los rodea, la frecuencia de resonancia pasa a ser \begin{equation}\label{ec12} \nu=\frac{\gamma}{2\pi}(1-\sigma)B_0 \end{equation} Los núcleos con distinto entorno químico presentan una constante de apantallamiento diferente, generando diferentes señales en el espectro de RMN.
- Detalles
- Germán Fernández
- RESONANCIA MAGNÉTICA NUCLEAR (RMN)
- Visto: 32073
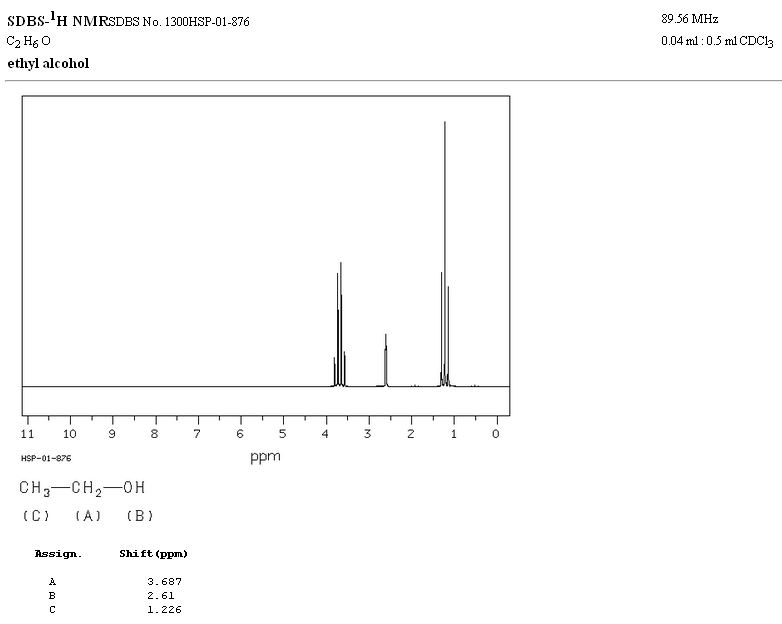
En el espectro de RMN del etanol se observan tres señales diferentes, debido a la existencia de 3 tipos de hidrógenos con distinto entorno químico. Los hidrógenos A están más desapantallados que los C debido a la presencia del oxígeno (átomo electonegativo que retira densidad electrónica). El entorno químico del hidrógeno B, unido directamente al oxígeno, también es diferente resonando a una frecuencia distinta a los anteriores.
- Detalles
- Germán Fernández
- RESONANCIA MAGNÉTICA NUCLEAR (RMN)
- Visto: 30850
Las señales del espectro de RMN se miden en una escala independiente del campo magnético aplicado, llamada desplazamiento químico y representada por la letra $\delta$. Independientemente del campo magnético al que trabaje el espectrofotómetro, las señales de un compuesto químico se obtienen siempre a los mismos valores de $\delta$. \begin{equation} \delta=\frac{\nu_{muestra}-\nu_{referencia}}{\nu_{referencia}}\cdot 10^6 \end{equation} Por definición se toma como cero de la escala de desplazamiento químico la señal del tetrametilsilano ($Si(CH_3)_4$). Vamos a calcular el desplazamiento químico para el $CH_3Br$ sabiendo que en un aparato de 90 MHz la frecuencia de absorción ocurre a 90 000 237 Hz. \begin{equation} \delta =\frac{90 000 237 - 90 000 000}{90 000 000}\cdot 10^{6}=2,63 \end{equation} En un espectrofotómetro que trabaje a 300 MHz la absorción se produce a 300 000 790 Hz, repitiendo el cálculo anterior se obtiene el mismo desplazamiento químico.\\ Los hidrógenos más desapantallados salen a desplazamientos mayores: $CH_3Br\rightarrow \delta =2,63$; $CH_2Br_2\rightarrow \delta =4,90$; $CHBr_3\rightarrow \delta = 6,82$
- Detalles
- Germán Fernández
- RESONANCIA MAGNÉTICA NUCLEAR (RMN)
- Visto: 44201
En la siguiente tabla pueden observarse los rangos en que aparecen las señales de RMN para diferentes tipos de hidrógenos.
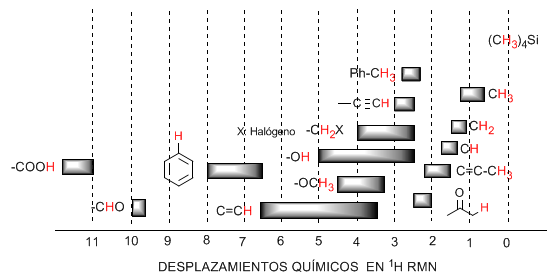
♦ Los hidrógenos situados sobre cadenas alifáticas presentan valores de $\delta$ próximos a 1. Aunmentando ligeramente al pasar de carbonos primarios a secundarios o terciarios.
♦ Los hidrógenos alílicos se localizan entre 1,5 y 2,1.
♦ Los hidrógenos alfa respecto a carbonilos y derivados de ácido se sitúan entre 2 y 2,5.
♦ Los hidrógenos bencílicos entre 2,3 y 2,7.
♦ El hidrógeno de alquinos terminales entre 2,5 y 3.
♦ Hidrógenos unidos a carbonos con halógenos entre 2,5 y 4 dependiendo de la electronegatividad del halógeno
♦ Los hidrógenos del grupo hidroxilo entre 2,5 y 5. Rango muy amplio debido a la formación de puentes de hidrógeno.
♦ Hidrógenos de carbonos unidos a oxígeno tipo éter entre 3,3 y 4,5.
♦ Hidrógenos olefínicos entre 3,5 y 6,5.
♦ Hidrógenos unidos a sistemas aromáticos entre 6,5 y 8.
♦ Hidrógeno de aldehídos 9,5-10
♦ Hidrógeno del grupo ácido carboxílico por encima de 11.
- Detalles
- Germán Fernández
- RESONANCIA MAGNÉTICA NUCLEAR (RMN)
- Visto: 20906
Los sustituyentes electronegativos retiran densidad electrónica, desapantallando los hidrógenos y desplazan la señal hacia valores altos de $\delta$.
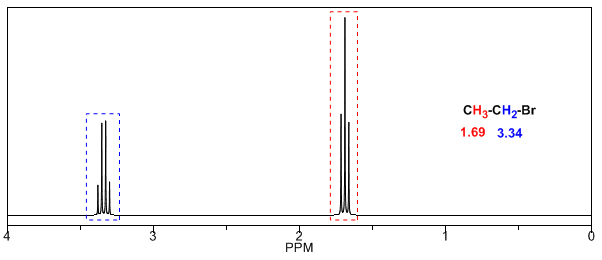
En la siguiente tabla puede verse la influencia de diferentes átomos sobre la señal de los hidrógenos del metilo.
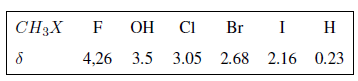
Como puede observarse en la tabla a mayor electronegatividad del grupo X mayor desplazamiento químico.
El efecto de los grupos electronegativos es aditivo, a mayor número de grupos el protón está más desapantallado y el desplazamiento es mayor
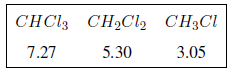
El efecto inductivo se propaga a lo largo de las cadenas, disminuyendo su efecto con la distancia, como puede observarse en la siguiente tabla.
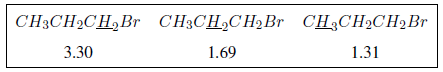
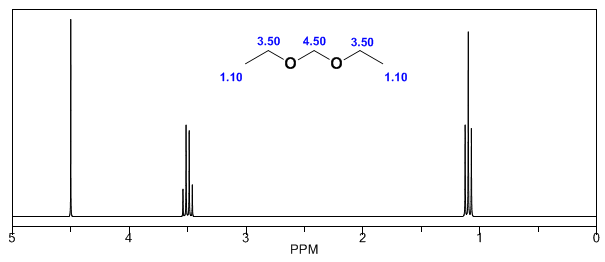
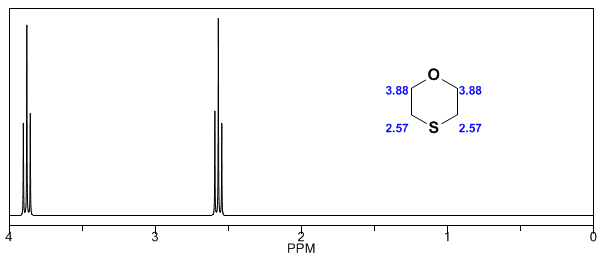
En los siguientes espectros puede observarse los efectos comentados anteriormente sobre los desplazamientos químicos.
- Detalles
- Germán Fernández
- RESONANCIA MAGNÉTICA NUCLEAR (RMN)
- Visto: 30940
Los protones próximos a dobles enlaces y anillos aromáticos están especialmente desapantallados debido al campo magnético inducido por las corrientes electrónicas de estos sistemas. El campo inducido se suma al aplicado, produciendo un desplazamiento superior al esperado.
En la siguiente imagen podemos ver la cirulación electrónica (curvas en negrita) y el campo magnético inducido (lineas a trazos) para un alqueno y un carbonilo. Obsérvese como en la región del protón el campo magnético inducido tiene identica dirección y sentido que el aplicado.
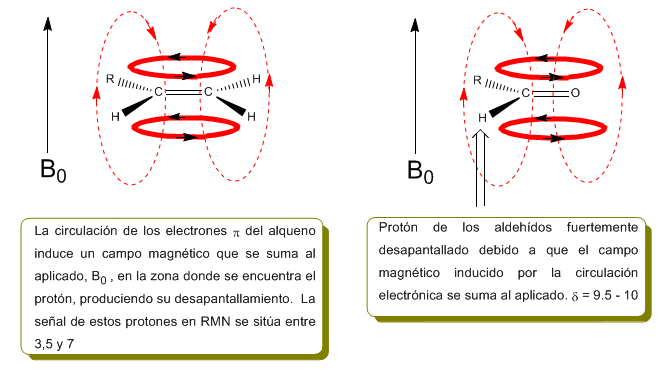
En el caso del benceno se observa una situación análoga. Sin embargo, en los alquinos la circulación electrónica induce un campo magnético que se opone al aplicado en la zona del protón. Los hidrógenos acetilénicos están apantallados con señales en el espectro de RMN a desplazamientos bajos.
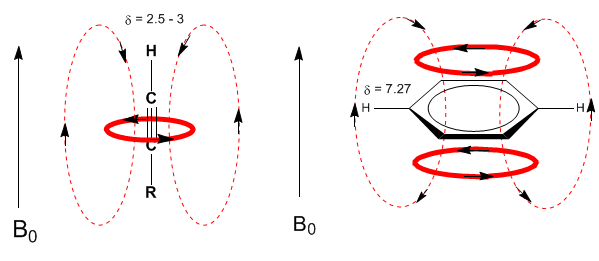
A continuación, añado algunos espectros de alquenos, alquinos y aromáticos.
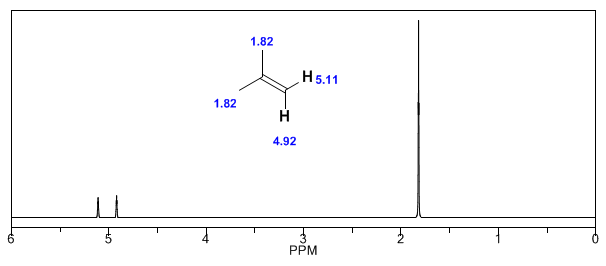
Obsérvese como los campos inducidos aumentan considerablemente los deplazamientos del protón olefínico, viéndose también afectadas las posiciones alílicas.
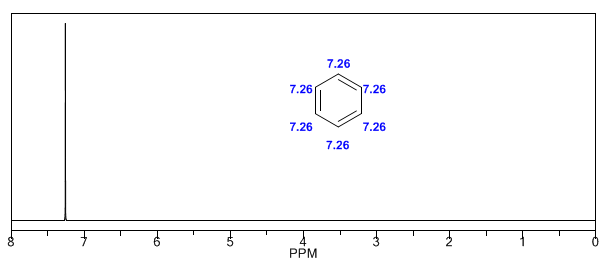
Los hidrógenos aromáticos están fuertemente desapantallados debido al campo inducido por las corrientes del anillo.
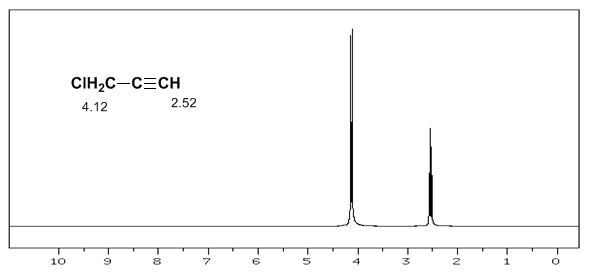
El hidrógeno acetilénico presenta un desplazamiento bajo, debido a que las corrientes producen un campo magnético que se opone al aplicado.
- Detalles
- Germán Fernández
- RESONANCIA MAGNÉTICA NUCLEAR (RMN)
- Visto: 16273
La formación de enlaces de hidrógeno produce mayores valores de desplazamiento. La presencia de hidrógenos ácidos puede detectarse por adición de agua deuterada, que produce el intercambio del hidrógeno ácido por deuterio, con la consiguiente desaparición de la señal. \begin{equation} CH_3OH + D_2O \rightleftharpoons CH_3OD + HDO \end{equation} Los desplazamientos hidrógenos ácidos más comunes en las moléculas orgánicas son:
- Ácidos carboxílicos (RCOOH) $\delta$ = 10 - 12 ppm
- Aminas ($R-NH_2$) $\delta$ = 0.5 - 5 ppm
- Amidas ($RCONH_2$) $\delta$ = 5-8 ppm
- Alcoholes (ROH) $\delta$ = 0.5 - 5 ppm
- Fenoles (Ph-OH) $\delta$ = 4 - 7 ppm
- Detalles
- Germán Fernández
- RESONANCIA MAGNÉTICA NUCLEAR (RMN)
- Visto: 40194
La información estructural del RMN deriva de dos factores: los diferentes desplazamientos observados dependiendo del ambiente químico que rodea al protón y del acoplamiento entre los espines de protones próximos, que produce el desdoblamiento de las señales.
Aunque algunas señales del espectro son picos simples, es habitual encontrar señales compuestas por varios picos muy próximos, que se nombran con la siguiente notación: singulete (s), doblete (d), triplete (t), cuatriplete (c), quintuplete (q), sextuplete (sx) y septuplete (sp), señales complejas se las designa como multipletes. El valor de $\delta$ de estas señales se asigna al centro de las mismas, salvo que el multiplete sea irregular en cuyo caso se indica el intervalo.
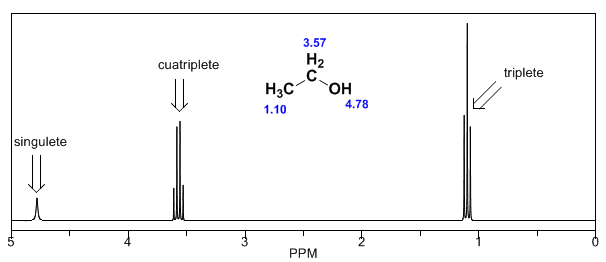
En el espectro del etanol puede observarse que el hidrógeno hidroxílico produce un singulete, la pareja de hidrógenos del carbono uno dan lugar a un cuatriplete y los tres hidrógenos del carbono dos producen un triplete.
Explicación del acoplamiento espín-espín.
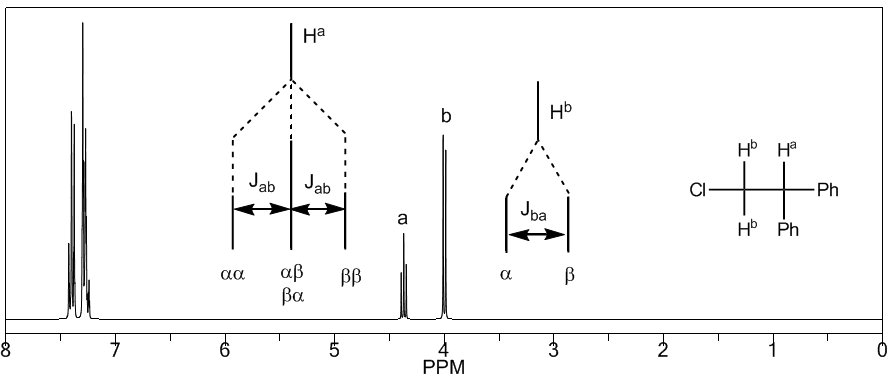
Para comprender el desdoblamiento de las señales debido al acoplamiento espín-espín vamos a estudiar el espectro del 1,1-dicloro-2,2-difeniletano ($Cl_2CH^{a}CH^{b}Ph_2$).
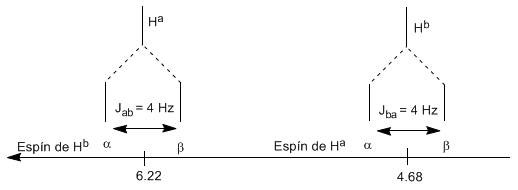
El proton $H^a$ sometido a un campo magnético $B_0$ produce una señal a $\delta_a=6,22 ppm$. Sin embargo, el protón $H_b$ genera un pequeño campo magnético que afecta al protón $H_a$. Aproximadamente la mitad de las moléculas tienen el protón $H_b$ alineado con el campo aplicado (espín alfa) y la otra mitad lo tienen orientado en contra del campo (espín beta). Cuando $H_b$ tiene espín $\alpha$, $H_a$ se ve sometido a un campo ligeramente mayor y resuena a una mayor frecuencia ($\delta$ ligeramente mayor). Cuando $H_b$ tiene espín $\beta$, $H_a$ se ve sometido a un campo ligeramente menor y resuena a menor frecuencia ($\delta$ ligéramente menor), lo cual produce el desdoblemiento del pico inicial en dos señales separados por una distancia de 4 Hz, llamada constante de acoplamiento (J). Este mismo razonamiento se puede realizar para el proton $H_b$.
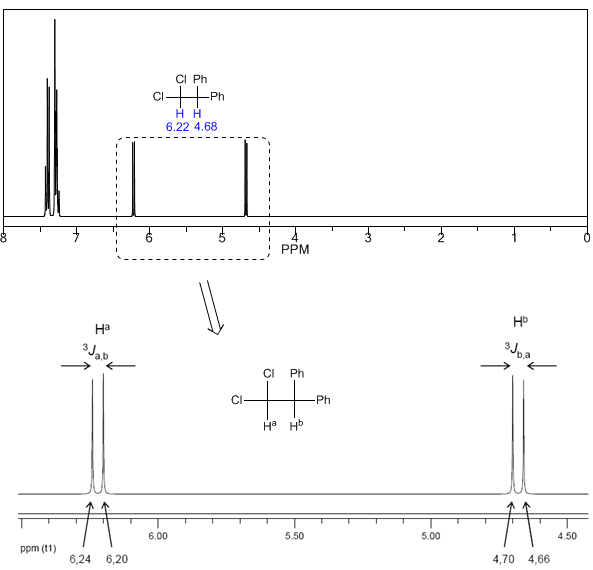
A continuación, estudiaremos el acoplamiento de un hidrógneno $H^a$ que posee dos hidrógenos vecinos $H^b$. En esta situación se observa el desdoblamiento de la señal del hidrógeno $H^a$ en tres picos (triplete), siendo el pico central el doble más intenso que los de los extremos. Por su parte los hidrógenos $H^b$ acoplan con el $H^a$ produciendo dos picos de igual intensidad (doblete)
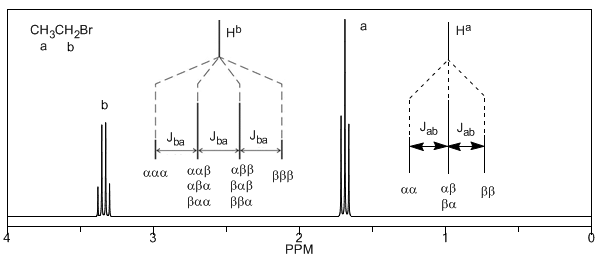
Por último, discutiremos el acoplamiento de un protón con tres protones vecinos equivalentes. En este caso se observa una señal formada por cuatro picos (cuatriplete). Los picos centrales poseen el triple de intensidad que los picos de los extremos.
- Detalles
- Germán Fernández
- RESONANCIA MAGNÉTICA NUCLEAR (RMN)
- Visto: 22912
De la discusión anterior puede deducirse que un protón produce una señal con un número de picos una unidad superior al número de hidrógenos vecinos. En la siguiente imagen podemos observar los picos que produce un hidrógeno $H^b$ al acoplarse con un número de hidrógenos variables $H^a$
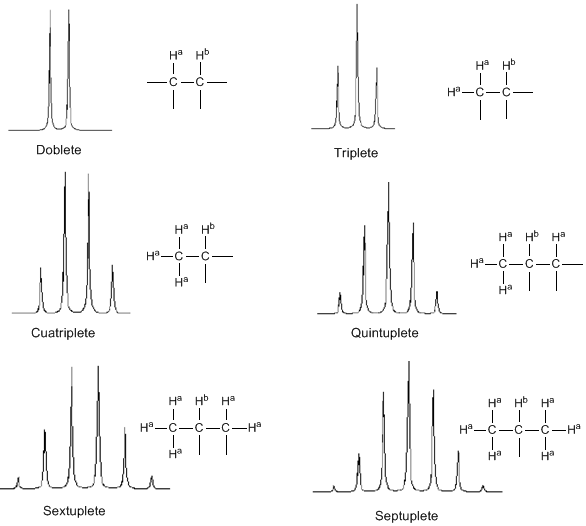
La intensidad de los picos de una señal vienen dados por el triángulo de Pascal (Tartaglia)
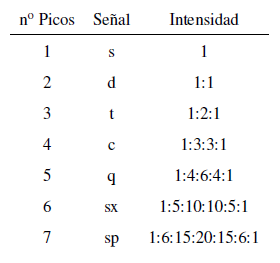
Deben tenerse en cuenta dos consideraciones al aplicar la regla N+1:
- En moléculas del tipo $A-CH_{2}^{a}-CH_{2}^{b}-CH_{2}^{a}-A$ los protones $H^b$ aparecen como un quintuplete.
- En moléculas del tipo $A-CH_2-CH_2-A$, los cuatro protones son equivalentes y dan un singulete.
- Detalles
- Germán Fernández
- RESONANCIA MAGNÉTICA NUCLEAR (RMN)
- Visto: 14911
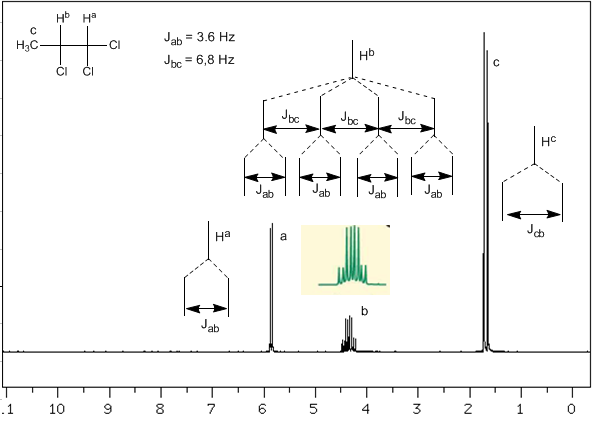
Ahora analizaremos una situación más compleja en la cual los núcleos $H^b$ presentan diferentes constantes de acoplamiento con los núcleos vecinos $H^c$ y $H^a$. Sabiendo que las constantes de acoplamiento entre estos tres núcleos son $J_{ab}=3.6\;Hz$ y $J_{bc}=6.8\;Hz$, para obtener la señal de $H^b$ lo acoplamos primero con $H^c$ (mayor constante de acoplamiento), dando cuatro picos (regla N+1), que a continuación se acoplan con $H^a$ desdoblándose cada uno en dos picos. En total se obtiene una señal formada por ocho picos.
- Detalles
- Germán Fernández
- RESONANCIA MAGNÉTICA NUCLEAR (RMN)
- Visto: 18148
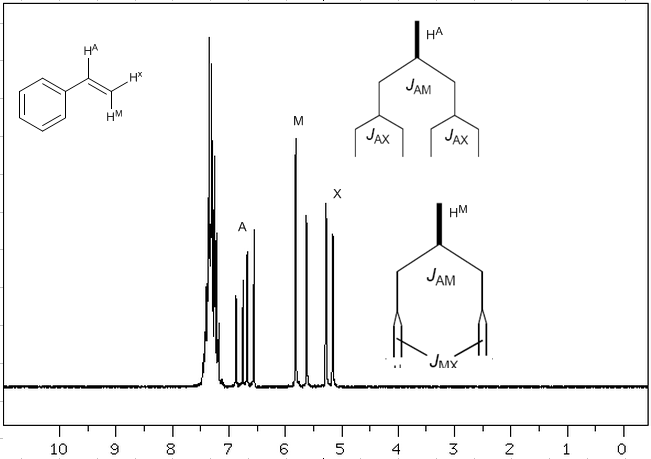
Teniendo en cuenta que el orden de constantes de acoplamiento en alquenos es $J_{trans}>J_{cis}>J_{geminal}$, los árboles de acoplamiento para los hidrógenos $H^a$ y $H^M$ son los indicados en el espectro. ¿Serías capaz de dibujar el arbol para $H^x$?