En mecánica cuántica el momento angular magnético en dirección z viene dado por $L_z=m_I\hbar$. El núcleo con $m_I=1/2$ tiene $L_z=1/2\hbar$, mientras que el núcleo con $m_I=-1/2$ tiene $L_z=-1/2\hbar$. El momento magnético en esta dirección es $\mu_z=\gamma L_z$.

Estas ecuaciones nos permiten determinar la energía de ambos niveles. \begin{equation}\label{ec4} E=-\mu_zB_0=-\gamma m_I\hbar B_0 \end{equation} Ahora podemos calcular la diferencia de energía entre ambos niveles \begin{equation}\label{ec6} \Delta E=-\gamma (-1/2)\hbar B_0 + \gamma 1/2\hbar B_0=\gamma\hbar B_0 \end{equation}

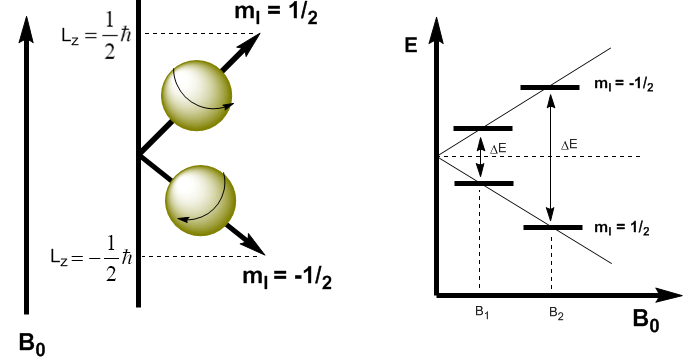
Como puede observarse en la ecuación (\ref{ec6}) la diferencia de energía depende del campo magnético aplicado. Si el campo magnético es bajo, $\Delta E$ es pequeño y la diferencia de población entre ambos niveles también es baja, lo que provoca un problema de sensibilidad. A campos magnéticos elevados tenemos una separación importante entre niveles lo que da lugar a una diferencia de población alta, obteniéndose una mayor sensibilidad.