ESPECTROSCOPÍA DE INFRARROJO
- Detalles
- Germán Fernández
- ESPECTROSCOPÍA DE INFRARROJO
- Visto: 57539
Los fotones de radiación infrarroja son absorbidos por los enlaces de una molécula pasando a niveles vibracionales superiores.
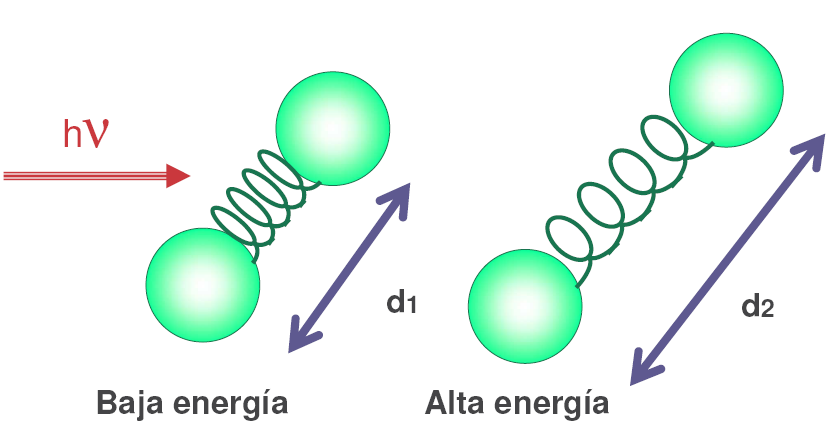
Cada tipo de enlace absorbe radiación infrarroja a una frecuencia distinta, lo que permite determinar que tipo de grupos funcionales posee la molécula en estudio. Los espectrofotómetros de infrarrojo trabajan en el infrarrojo medio y hacen un barrido desde los 4000 $cm^{-1}$ hasta los 400 $cm^{-1}$
- Detalles
- Germán Fernández
- ESPECTROSCOPÍA DE INFRARROJO
- Visto: 40967
Para que una molécula absorba radiación infrarroja deben cumplirse dos condiciones:
- La frecuencia de la radiación (fotón) debe ser la adecuada para permitir la transición entre estados vibracionales. Dicho de otro modo, la frecuencia de la radiación debe coincidir con la frecuencia natural del movimiento vibracional.
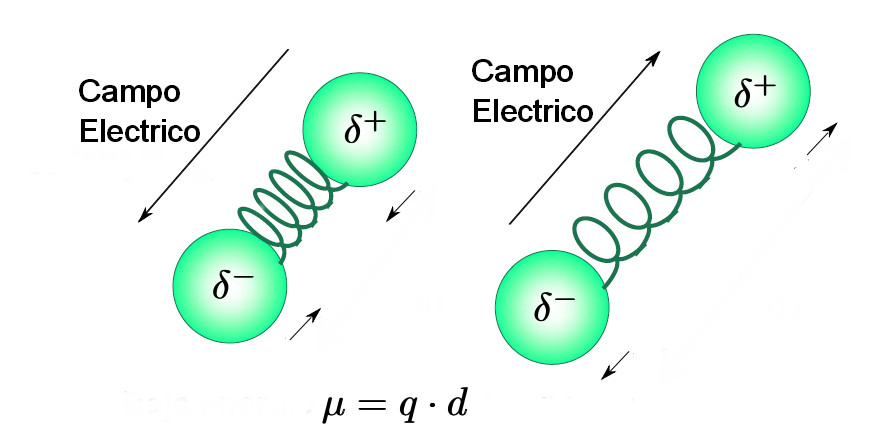
- Una molécula sólo absorbe radiación infrarroja cuando su momento dipolar interacciona con el campo electrico de la onda, variando en fase con este. Como es lógico este acoplamiento sólo es posible si las frecuencias de la radiación y la vibración del enlace coinciden. Por ello, moléculas apolares no absorben en el infrarrojo y moléculas poco polares dan lugar a absorciones muy débiles.
- Regla de selección de la espectroscopía infrarroja: "sólamente aquellos enlaces cuya vibración provoque un cambio en el momento dipolar de la molécula absorben en el infrarrojo".
- Detalles
- Germán Fernández
- ESPECTROSCOPÍA DE INFRARROJO
- Visto: 24984
Las vibraciones moleculares pueden estudiarse con el modelo del oscilador armónico cuántico. La energía viene dada por:
\begin{equation}\label{energia-oscilador} E_v=\left(v+\frac{1}{2}\right)h\nu \end{equation}
Los distintos niveles de energía vienen dados por el número cuántico v, que toma valores 0.1.2.3.4.....
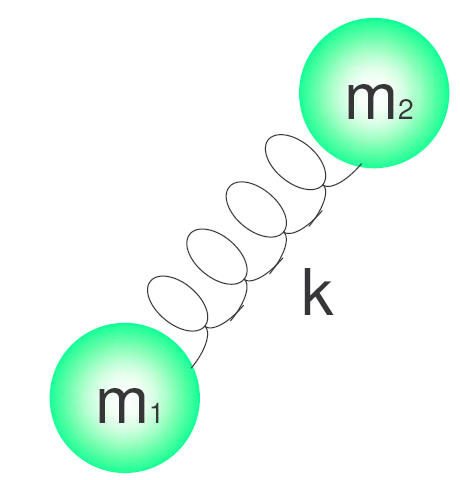
h es la constante de Planck y $\nu$ la frecuencia del oscilador que viene dada por la expresión:\begin{equation} \nu=\frac{1}{2\pi}\sqrt{\frac{k}{\mu}} \end{equation} Donde k es la constante de fuerza del muelle y $\mu$ la masa reducida del sistema. $\mu=\frac{m_1m_2}{m_1+m_2}$.
Dividiendo la frecuencia entre la velocidad de la luz se obtiene número de ondas $\bar{\nu}$ \begin{equation}\label{numero-ondas} \bar{\nu}=\frac{1}{2\pi c}\sqrt{\frac{k}{\mu}} \end{equation} El estudio de la ecuación (\ref{numero-ondas}) nos permitirá predicir a qué número de ondas absorben radiación infrarroja los enlaces de una molécula. Esta ecuación sólo es aplicable a las vibraciones de tensión.
- Detalles
- Germán Fernández
- ESPECTROSCOPÍA DE INFRARROJO
- Visto: 54892
Vibración de tensión (stretching). Los átomos unidos por enlaces simples, dobles o triples se acercan y alejan siguiendo la dirección del enlace, igual que oscilan dos masas unidas por un muelle.
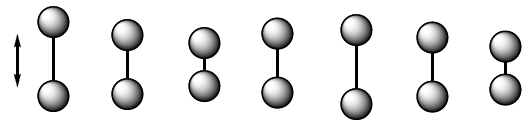Vibración de Tensión
- Detalles
- Germán Fernández
- ESPECTROSCOPÍA DE INFRARROJO
- Visto: 21044
- Absorciones fundamentales, son transiciones vibracionales desde el estado fundamental al primer estado excitado. Dan lugar a las bandas de mayor intensidad.
- Sobretonos, son transiciones vibracionales desde el estado fundamental a estados excitados superiores. Las frecuencias de absorción son $2/nu,3\nu...$ siendo $\nu$ la frecuencia de la absorción fundamental.
- Bandas de combinación, resultan del acoplamiento de 2 bandas $\nu_1$ y $\nu_2$ para dar lugar a una nueva banda de frecuencia $\nu_{comb}=\nu_1 + \nu_2$
- Bandas de diferencia, , resultan del acoplamiento de 2 bandas $\nu_1$ y $\nu_2$ para dar lugar a una nueva banda de frecuencia $\nu_{comb}=\nu_1 - \nu_2$
- Resonancia de Fermi, resultan del acoplamiento de una banda de absorción fundamental con un sobretono o una banda de combinación.
